Tangent Bundle

Every smooth manifold 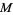 has a tangent bundle 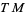, which consists of the tangent space  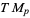at all points  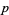in 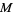. Since a tangent space  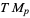is the set of all tangent vectors to  at 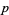, the tangent bundle is the collection of all tangent vectors, along with the information of the point to which they are tangent.

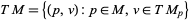(1)

The tangent bundle is a special case of a vector bundle. As a bundle it has bundle rank , where  is the dimension of . A coordinate chart on 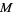 provides a trivialization for 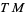. In the coordinates, 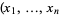), the vector fields 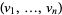, where 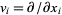, span the tangent vectors at every point (in the coordinate chart). The transition function from these coordinates to another set of coordinates is given by the Jacobian of the coordinate change.

For example, on the unit sphere, at the point 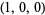 there are two different coordinate charts defined on the same hemisphere,  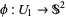and ,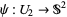

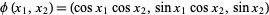(2)

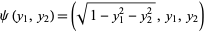(3)

with 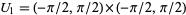 and 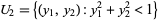. The map between the coordinate charts is .

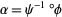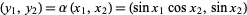(4)

The Jacobian of 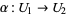 is given by the matrix-valued function

(5)

which has determinant 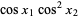 and so is invertible on .

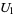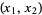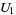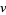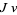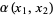The tangent vectors transform by the Jacobian. At the point  in , a tangent vector  corresponds to the tangent vector  at  in 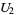. These two are just different versions of the same element of the tangent bundle.