


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-8-2021
Date: 29-6-2021
Date: 14-6-2021
|

Two mathematical objects are said to be homotopic if one can be continuously deformed into the other. For example, the real line is homotopic to a single point, as is any tree. However, the circle is not contractible, but is homotopic to a solid torus. The basic version of homotopy is between maps. Two maps 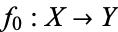 and
and 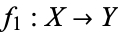 are homotopic if there is a continuous map
are homotopic if there is a continuous map
![F:X×[0,1]->Y](https://mathworld.wolfram.com/images/equations/Homotopic/NumberedEquation1.gif) |
such that 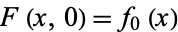 and
and 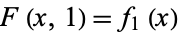 .
.

Whether or not two subsets are homotopic depends on the ambient space. For example, in the plane, the unit circle is homotopic to a point, but not in the punctured plane 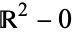 . The puncture can be thought of as an obstacle.
. The puncture can be thought of as an obstacle.
However, there is a way to compare two spaces via homotopy without ambient spaces. Two spaces 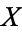 and
and 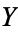 are homotopy equivalent if there are maps
are homotopy equivalent if there are maps 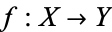 and
and 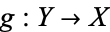 such that the composition
such that the composition 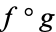 is homotopic to the identity map of
is homotopic to the identity map of 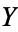 and
and 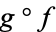 is homotopic to the identity map of
is homotopic to the identity map of 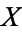 . For example, the circle is not homotopic to a point, for then the constant map would be homotopic to the identity map of a circle, which is impossible because they have different Brouwer degrees.
. For example, the circle is not homotopic to a point, for then the constant map would be homotopic to the identity map of a circle, which is impossible because they have different Brouwer degrees.
REFERENCES:
Aubry, M. Homotopy Theory and Models. Boston, MA: Birkhäuser, 1995.
Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.
Krantz, S. G. "The Concept of Homotopy" §10.3.2 in Handbook of Complex Variables. Boston, MA: Birkhäuser, pp. 132-133, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|