


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-6-2017
Date: 11-7-2021
Date: 10-5-2021
|
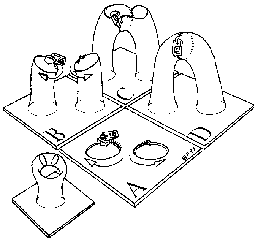
A handle is a topological structure which can be thought of as the object produced by puncturing a surface twice, attaching a zip around each puncture travelling in opposite directions, pulling the edges of the zips together, and then zipping up.
Handles are to manifolds as cells are to CW-complexes. If 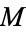 is a manifold together with a
is a manifold together with a 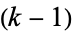 -sphere
-sphere 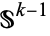 embedded in its boundary with a trivial tubular neighborhood, we attach a
embedded in its boundary with a trivial tubular neighborhood, we attach a 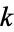 -handle to
-handle to 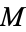 by gluing the tubular neighborhood of the
by gluing the tubular neighborhood of the 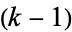 -sphere
-sphere 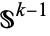 to the tubular neighborhood of the standard
to the tubular neighborhood of the standard 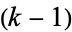 -sphere
-sphere 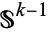 in the dim(
in the dim(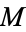 )-dimensional disk. In this way, attaching a
)-dimensional disk. In this way, attaching a 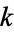 -handle is essentially just the process of attaching a fattened-up
-handle is essentially just the process of attaching a fattened-up 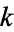 -disk to
-disk to 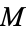 along the
along the 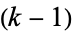 -sphere
-sphere 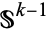 . The embedded disk in this new manifold is called the
. The embedded disk in this new manifold is called the 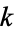 -handle in the union of
-handle in the union of 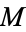 and the handle.
and the handle.
Dyck's theorem states that handles and cross-handles are equivalent in the presence of a cross-cap.
REFERENCES:
Francis, G. K. and Weeks, J. R. "Conway's ZIP Proof." Amer. Math. Monthly 106, 393-399, 1999.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|