
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2021
Date: 14-3-2021
Date: 10-4-2021
|
Let 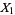 and
and 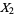 be the number of successes in variates taken from two populations. Define
be the number of successes in variates taken from two populations. Define
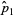 |
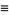 |
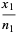 |
(1) |
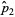 |
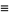 |
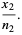 |
(2) |
The estimator of the difference is then 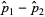 . Doing a so-called
. Doing a so-called 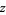 -transform,
-transform,
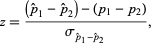 |
(3) |
where
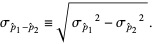 |
(4) |
The standard error is
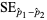 |
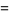 |
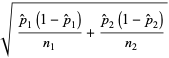 |
(5) |
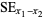 |
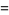 |
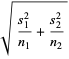 |
(6) |
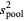 |
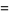 |
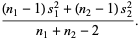 |
(7) |
REFERENCES:
Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, pp. 162-171, 1993.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|