


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-3-2021
Date: 23-3-2021
Date: 6-2-2021
|
Fisher's exact test is a statistical test used to determine if there are nonrandom associations between two categorical variables.
Let there exist two such variables 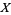 and
and 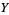 , with
, with 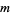 and
and 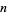 observed states, respectively. Now form an
observed states, respectively. Now form an 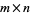 matrix in which the entries
matrix in which the entries 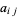 represent the number of observations in which
represent the number of observations in which 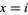 and
and 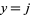 . Calculate the row and column sums
. Calculate the row and column sums 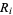 and
and 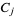 , respectively, and the total sum
, respectively, and the total sum
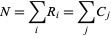 |
(1) |
of the matrix. Then calculate the conditional probability of getting the actual matrix given the particular row and column sums, given by
 |
(2) |
which is a multivariate generalization of the hypergeometric probability function. Now find all possible matrices of nonnegative integers consistent with the row and column sums 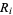 and
and 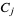 . For each one, calculate the associated conditional probability using (2), where the sum of these probabilities must be 1.
. For each one, calculate the associated conditional probability using (2), where the sum of these probabilities must be 1.
To compute the P-value of the test, the tables must then be ordered by some criterion that measures dependence, and those tables that represent equal or greater deviation from independence than the observed table are the ones whose probabilities are added together. There are a variety of criteria that can be used to measure dependence. In the 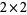 case, which is the one Fisher looked at when he developed the exact test, either the Pearson chi-square or the difference in proportions (which are equivalent) is typically used. Other measures of association, such as the likelihood-ratio-test,
case, which is the one Fisher looked at when he developed the exact test, either the Pearson chi-square or the difference in proportions (which are equivalent) is typically used. Other measures of association, such as the likelihood-ratio-test, 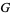 -squared, or any of the other measures typically used for association in contingency tables, can also be used.
-squared, or any of the other measures typically used for association in contingency tables, can also be used.
The test is most commonly applied to 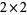 matrices, and is computationally unwieldy for large
matrices, and is computationally unwieldy for large 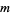 or
or 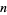 . For tables larger than
. For tables larger than 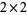 , the difference in proportion can no longer be used, but the other measures mentioned above remain applicable (and in practice, the Pearson statistic is most often used to order the tables). In the case of the
, the difference in proportion can no longer be used, but the other measures mentioned above remain applicable (and in practice, the Pearson statistic is most often used to order the tables). In the case of the 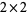 matrix, the P-value of the test can be simply computed by the sum of all
matrix, the P-value of the test can be simply computed by the sum of all 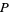 -values which are
-values which are 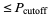 .
.
For an example application of the 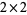 test, let
test, let 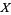 be a journal, say either Mathematics Magazine or Science, and let
be a journal, say either Mathematics Magazine or Science, and let 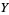 be the number of articles on the topics of mathematics and biology appearing in a given issue of one of these journals. If Mathematics Magazine has five articles on math and one on biology, and Science has none on math and four on biology, then the relevant matrix would be
be the number of articles on the topics of mathematics and biology appearing in a given issue of one of these journals. If Mathematics Magazine has five articles on math and one on biology, and Science has none on math and four on biology, then the relevant matrix would be
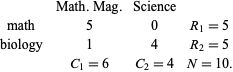 |
(3) |
Computing 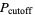 gives
gives
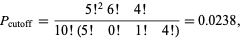 |
(4) |
and the other possible matrices and their 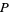 s are
s are
![[4 1; 2 3] P](https://mathworld.wolfram.com/images/equations/FishersExactTest/Inline27.gif) |
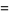 |
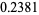 |
(5) |
![[3 2; 3 2] P](https://mathworld.wolfram.com/images/equations/FishersExactTest/Inline30.gif) |
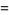 |
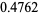 |
(6) |
![[2 3; 4 1] P](https://mathworld.wolfram.com/images/equations/FishersExactTest/Inline33.gif) |
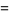 |
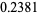 |
(7) |
![[1 4; 5 0] P](https://mathworld.wolfram.com/images/equations/FishersExactTest/Inline36.gif) |
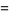 |
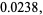 |
(8) |
which indeed sum to 1, as required. The sum of 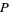 -values less than or equal to
-values less than or equal to 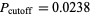 is then 0.0476 which, because it is less than 0.05, is significant. Therefore, in this case, there would be a statistically significant association between the journal and type of article appearing.
is then 0.0476 which, because it is less than 0.05, is significant. Therefore, in this case, there would be a statistically significant association between the journal and type of article appearing.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|