


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 16-9-2020
Date: 13-9-2020
Date: 13-9-2020
|
Intersection of two straight lines
Another interpolation situation involves two known points in a two-dimensional phase space, an assumed straight line between them, and another straight line that intersects the first line (Fig. 1). The job is to estimate the coordinates of the point where the two lines intersect. The two points (e.g. A and B in Fig. 1) were measured at successive times, so the problem again boils down to estimating coordinate values at some intermediate time.
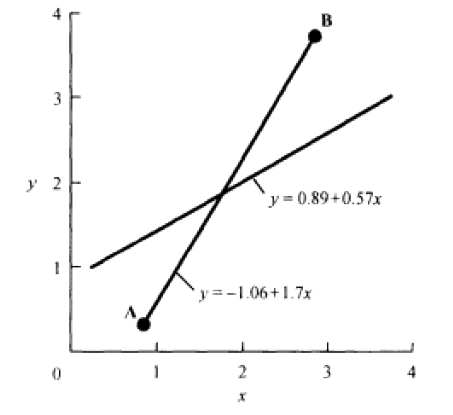
Figure 1: Intersection of two straight lines in two-dimensional space.
The solution is straightforward, although it requires knowing the parameter values in the equations of both lines. Any of the three methods discussed above can give those parameters. Obtaining them leaves two equations (one for each line), with unknown x and y values in each equation. Exactly at (and only at) the point of intersection, the two equations give the same x and y values. Hence, for that particular point the x and y values (or equivalent expressions of each) are interchangeable between the two equations. We can then get the desired coordinates by equating one equation to the other, that is, by solving them simultaneously.
To illustrate with Figure 1, say the equations of the two intersecting straight lines (with parameters determined by any of the methods explained earlier) are: y=-1.06+1.7x and y=0.89+0.57x. To find the unique pair of x and y values that are common to both lines, we solve the equations simultaneously. We can do that either by equating the two or by subtracting the lower equation from the upper. Either of those approaches eliminates y. For our example, that leaves 0=-1.95+1.13x, or x=1.73. We then use the x value and the equation of either line to get y. For instance, with the second equation we have y=0.89+0.57 (1.73) or y=1.88. Hence, the two lines cross at x=1.73, y=1.88.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|