Mermin–Wagner theorem

The derivation of the spin-wave dispersion has been based on the existence of a ferromagnetic state in an isotropic chain, or a three-dimensional lattice. The assumptions warrant scrutiny. The number of magnons excited at a temperature T is given by

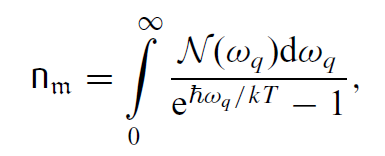
where the density of states for magnons N(ω_q ) in one, two and three dimensions varies as ω^−1/2_q , ω^o_q= constant and ω^1/2_q , respectively. The argument is similar to that for the electron gas, which has similar dispersion relations. Setting x = hω_q/k_BT , the integral in three dimensions varies as (kBT/h)^3/2  ∫^∞₀ x^1/2d³x/(e^x − 1), whence comes the Bloch T ^3/2 .
However, the integrals diverge at finite temperature in one and two dimensions. The ferromagnetically ordered state should be unstable in dimensions lower than 3. This is the Mermin–Wagner theorem. Magnetic order is possible in the Heisenberg model in three dimensions, but not in one or two. The linear chain,
our example of spin-wave dispersion, cannot order except at T = 0 K.
The consequences of this theorem are not as catastrophic as they seem at first sight. The divergence is avoided if there is some anisotropy in the system,which creates a gap in the spin-wave spectrum at q = 0; the lower limit of integration is then greater than zero and the divergence is avoided. Some anisotropy is always caused by crystal field or dipolar interactions. Two-dimensional ferromagnetic layers do exist in reality.