دوار القمة الغير متماثل The Asymmetric Top

ان عزوم القصور الذاتي الثلاثة لدوار قمة غير متماثل غير متساوية بالمقدار وفي هذه الحالة يعطى المؤثر الهاملتوني الدوراني بالعلاقة:

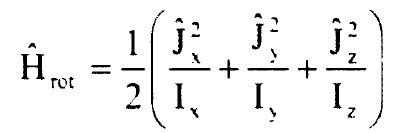..........(1)

ولا يمكن التعبير عن كما في حالة دوار القمة المتماثل ويجب تعيين الدوال الذاتية والقيم الذاتية للمؤثرين 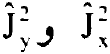ولتحقيق ذلك نكتب الدوال الموجية المجهولة Ψ للمؤثر 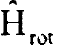كمجمع خطي  للدوال الذاتية (Ψ_n = Ψ_n (J, K, M للدوار المتماثل:

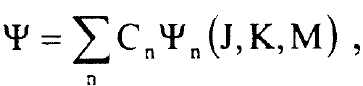.........(2)

ثم ندخلها في معادلة شرودنجر:

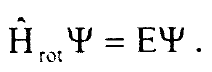...........(3)

ويمكن التعبير عن مقياس عدم التماثل باعلومة عدم التماثل:

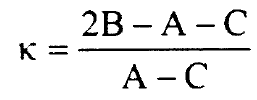............(4)

ولدوار القمة المتطاول B = C وتكون قيمة اعلومة عدم التماثل κ = -1 ولدوار القمة المتماثل المسطح A = B وقيمة اعلومة عدم التماثل = 1  κ ويحصل اكبر عدم تماثل عندما κ = 0 و.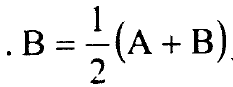

ومن المعادلة (1) نحصل على قيم الحد الطيفي الدورانية:

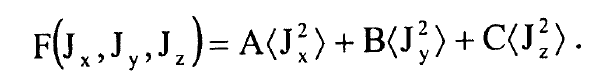..........(5)

وبعد التعويض عن اعلومة عدم التماثل κ  في المعادلة (5) نحصل على:

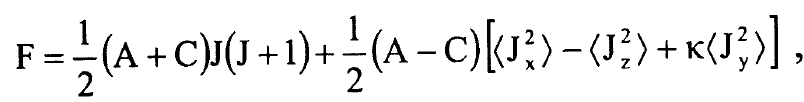...........(6)

والمعادلة (6) يمكن وضعها بالشكل:

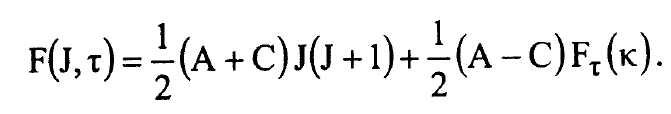.........(7)

وقد ادخلت الاعلومة τ لعد 2J+1 مستوى طاقة العائد الى نفس الزخم الزاوي الكلي J وفقا لمقدار طاقتهم وتاخذ القيم من J- الى J.

واذا رمزنا للقيمة المحددة للدوار المتطاول =-1 κ بالرمز K_a وللقيمة المحددة للدوار المفلطح =1κ بالرمز K_c يصبح التعبير عن الاعلومة τ بالشكل:

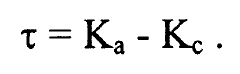.........(8)

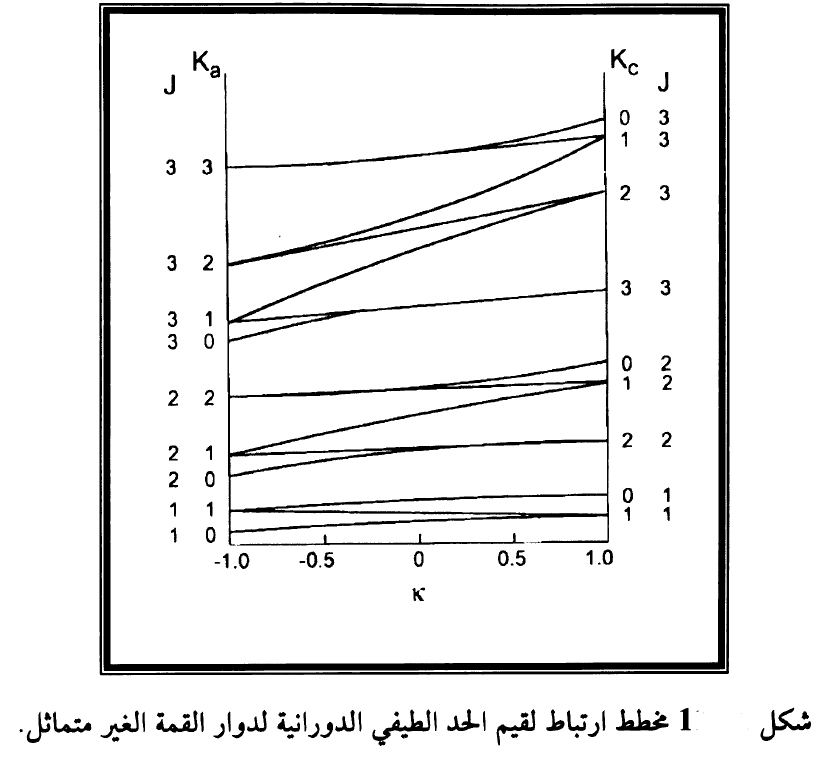
اذ يمكن ايجاد الدالة {F_τ(κ) = {J²_x} - {J²_z} + κ {J²_y بحساب القيم المتوقعة {J²_x},{J²_y} و{J²_z} باستخدام المعادلة (2) وفي شكل (1) مبين قيم الحد الطيفي لدوار قمة غير متماثل كدالة في اعلومة عدم التماثل k وتستخدم القيم المحددة K_a وK_c كثيرا بدلا من τ لتمييز مستوى طاقة، فمثلا يمكن كتابة J_{Ka, Kc} = 3_1,3 او J_τ = 3_-2.

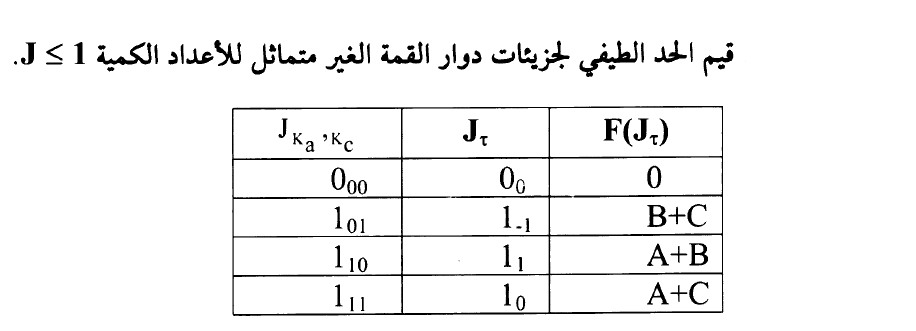
الجدول (1)

من مخطط الارتباط في شكل (1) نرى ان عدم التماثل يؤدي الى انشطار كل الحالات المتساوية الطاقة لدوار القمة المتماثل لقيمة K ≠ 0 الى مركبتين وفي جدول (1) مبين قيم الحد الطيفي للأعداد الكمية الدورانية J ≤ 1.

اخر الاخبار

اخبار العتبة العباسية المقدسة

خَدَمة العتبة العباسية المقدسة يؤدّون مراسم الممارسة العبادية بالتزامن مع ذكرى عاشوراء

المجمع العلمي يختتم مجالس العزاء لليالي العشر الأولى من المحرّم في بغداد

قسم الشؤون الدينية يقيم مجلسًا عزائيًّا لاستذكار أحداث اليوم الحادي عشر من المحرم

بعد انتهاء زيارة عاشوراء.. قسم بين الحرمين الشريفين يباشر بحملة تنظيف واسعة للساحة الوسطية

المزيد

الآخبار الصحية

تناول الجبن.. مفيد للجسم أم خطر يهدد صحتك؟

طبيبة أسنان تحذر.. لا تتجاهل هذه العلامة بعد التنظيف

يجب أن تأكل المزيد من الشمام هذا الصيف.. إليك السبب ؟

تأثير صحي كبير.. كم بيضة يجب أن تتناول يوميا؟

المزيد

الآخبار التكنلوجية

أداء خلايا البيروفسكايت الشمسية تحت الماء قد يزيد كفاءة تحويل الكهرباء

مسافة الأمان: أساس القيادة الآمنة وتجنب الحوادث

هل القيادة السريعة تعني استهلاك اكثر للوقود؟

لماذا يعتبر كوكب المريخ غير صالح للحياة؟

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon