طريقة Rydberg-Klein-Rees RKR

ان طريقة RKR طريقة جيدة وملائمة لايجاد منحني جهد V(r) من القيم الملاحظة لمستويات الطاقة الاهتزازية والثوابت الدورانية والمطلوب لاستخدام هذه الطريقة معرفة تغير الطاقة الاهتزازية والثابت الدوراني مع عدة الكم الاهتزازي v ثم يتم ايجاد نقاط تحول داخلية وخارجية (r₊ وr_- على منحني الجهد تعود لطاقة معينة) بالتقييم العددي لتكاملين متضمنين الدول G(v) وB(v) ويتم ايجاد منحني الجهد نقطة بعد نقطة.

وتعتمد صلاحية طريقة RKR على معيار تقريبي للقيم الذاتية لطاقة اهتزازية E ويدعى هذا المعيار شرط تكميم quantization؛ اي تقسيم نظام طاقة الى وحدات صغيرة، بور- سومرفيلد Bohr-Somerfeld الذي يمكن اشتقاقه بطريقة WKB ويعطى بالعلاقة:

...........(1)

هذا الشرط مطلوب لان طور الدالة Ψ من اليسار (داخل) نقطة التحول يجب ان يلائم طورها من اليمين (خارج) نقطة التحول:

..............(2)

.............(3)

ويجب ان يكون اختلاف الطور بمقدار nπ:

.............(4)

...............(5)

وفرق الطور  في المعادلتين (2) و(3) ياتي من طريقة لربط دالة WKB الموجية خارج البئر بتقريب دالة الجهد في نقطة التحول الى دالة خطية في r واستخدام الحل المضبوط لمعادلة شرودنجر لجهد خطي وهذا الاجراء ضروري لان تقريب WKB غير صحيح في نقاط التحول ويكون الربط صحيحا اذا:

وهذا المتطلب ينطبق تماما على دالة الجهد لمتذبذب توافقي.

تتضمن طريقة RKR تعريف لدالة خاصة A(E,J) مشتقاتها لجزيئة دول بسيطة لنقطتي التحول r₊ وr_- وهذه المشتقات يمكن التعبير عنها كتكاملات محتوية الدول G(v) وB(v) فقط ومتغير التكامل هو العدد الكمي الاهتزازي حيث G(v) الطاقة الاهتزازية وB(v) الثابت الدوراني معبر عنهما كدالة في v. ولان E=E (v,J) فمن الممكن تعريف v=v (E,J) وبالرغم من ان v وJ اعداد صحيحة لمستويات الطاقة الملاحظة فسوف تعتبر متغير مستمر في أية دالة. لنعرف الدالة A(E,J):

..................(6)

حيث E_min هي اقل طاقة للجهد V(r). نضع معادلة التكامل بالتجزئة بالشكل:

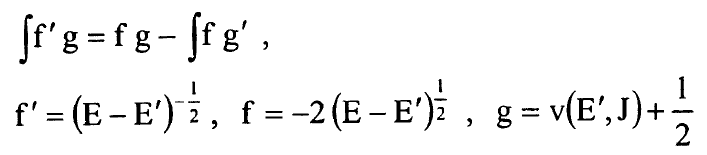................(7)

يتلائى الجزء f g لان f=0 عندما E=E وg=0 عندما v(E_min,J)= -1/2 لذا:

................(8)

وبتحويل المتغيرات:

...................(9)

وبأخذ المشتقة الاولى:

..............(10)

ولقيمة J=0:

...............(11)

وكذلك:

..................(12)

ولكن:

............(13)

................(14)

لقيمة J=0 فان بالضبط، لذا:

............(15)

وهكذا يصبح لدينا تعبير بسيط جدا لمشتقات A(E,J) بدلالة B(v) وG(v) وسنعيد الان التعبير عن هذه المشتقات بدلالة نقطتي التحول عند النقطة E ونعود الى تعريف A(E,J) في المعادلة (6) ونعيد كتابة شرط القيمة الذاتية في طريقة WKB في المعادلة (1) بالشكل:

................(16)

ونعيد كتابة V(r) كجمع حدين: الحد الاول U(r) يصف دالة الجهد لقيمة J=0 (في غياب الدوران) والحد الثاني يعود الى الطاقة الدورانية :

............(17)

والآن ندخل المعادلة (17) في المعادلة (6):

.............(18)

يتقارب التكامل في المعادلة (18) ويعطى بالمتساوية التكاملية الاتية:

..............(19)

لذا:

.............(20)

والمشتقة تساوي:

..........(21)

.................(22)

بجمع المعادلتين (21) و(11) نحصل على:

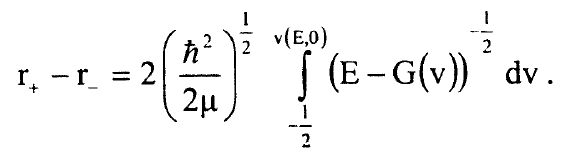...............(23)

وبجمع المعادلتين (22) و(15) نصل الى:

.............(24)

اذن لدينا معادلتان بمجهولين ويدعى التكامل في المعادلة (23) والتكامل في المعادلة (24) تكامل اجراء كلينf klein action وg ونكتبها بالشكل:

.........(25)

.............(26)

وباستخدام المعادلة التربيعية يمكن وضع المعادلتين (25) و(26) بالشكل:

.............(27)

اخر الاخبار

اخبار العتبة العباسية المقدسة

مجموعة مشاتل الكفيل: إضافة نحو 70 نوعًا جديدًا من المغروسات تتناسب مع الظروف المناخية المحلية

المجمَع العلمي يطلق الدورة التطويرية الخامسة لمعلمي التربية الإسلامية ومدرسيها في النجف الأشرف

خدمات إنسانية متنوّعة تقدّمها شعبة الشهداء والجرحى في مختلف المحافظات

قسم العلاقات العامة يطلق فعاليات مخيم البذرة الواعدة الخاص بأبناء المنتسبين

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon