


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 17-8-2020
Date: 2-3-2020
Date: 20-5-2020
|
A biquadratic number is a fourth power, 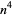 . The first few biquadratic numbers are 1, 16, 81, 256, 625, ... (OEIS A000583). The minimum number of biquadratic numbers needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1, 2, 3, 4, 5, ... (OEIS A002377), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of biquadratic numbers are 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, .... A brute-force algorithm for enumerating the biquadratic permutations of
. The first few biquadratic numbers are 1, 16, 81, 256, 625, ... (OEIS A000583). The minimum number of biquadratic numbers needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1, 2, 3, 4, 5, ... (OEIS A002377), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of biquadratic numbers are 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, .... A brute-force algorithm for enumerating the biquadratic permutations of 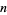 is repeated application of the greedy algorithm.
is repeated application of the greedy algorithm.
Every positive integer is expressible as a sum of (at most) 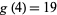 biquadratic numbers (Waring's problem). Davenport (1939) showed that
biquadratic numbers (Waring's problem). Davenport (1939) showed that 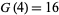 , meaning that all sufficiently large integers require only 16 biquadratic numbers. It is also known that every integer is a sum of at most 10 signed biquadrates (
, meaning that all sufficiently large integers require only 16 biquadratic numbers. It is also known that every integer is a sum of at most 10 signed biquadrates (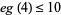 ; although it is not known if 10 can be reduced to 9). The following table gives the first few numbers which require 1, 2, 3, ..., 19 biquadratic numbers to represent them as a sum, with the sequences for 17, 18, and 19 being finite.
; although it is not known if 10 can be reduced to 9). The following table gives the first few numbers which require 1, 2, 3, ..., 19 biquadratic numbers to represent them as a sum, with the sequences for 17, 18, and 19 being finite.
| # | OEIS | numbers |
| 1 | A000583 | 1, 16, 81, 256, 625, 1296, 2401, 4096, ... |
| 2 | A003336 | 2, 17, 32, 82, 97, 162, 257, 272, ... |
| 3 | A003337 | 3, 18, 33, 48, 83, 98, 113, 163, ... |
| 4 | A003338 | 4, 19, 34, 49, 64, 84, 99, 114, 129, ... |
| 5 | A003339 | 5, 20, 35, 50, 65, 80, 85, 100, 115, ... |
| 6 | A003340 | 6, 21, 36, 51, 66, 86, 96, 101, 116, ... |
| 7 | A003341 | 7, 22, 37, 52, 67, 87, 102, 112, 117, ... |
| 8 | A003342 | 8, 23, 38, 53, 68, 88, 103, 118, 128, ... |
| 9 | A003343 | 9, 24, 39, 54, 69, 89, 104, 119, 134, ... |
| 10 | A003344 | 10, 25, 40, 55, 70, 90, 105, 120, 135, ... |
| 11 | A003345 | 11, 26, 41, 56, 71, 91, 106, 121, 136, ... |
| 12 | A003346 | 12, 27, 42, 57, 72, 92, 107, 122, 137, ... |
| 13 | A046044 | 13, 28, 43, 58, 73, 93, 108, 123, 138, ... |
| 14 | A046045 | 14, 29, 44, 59, 74, 94, 109, 124, 139, ... |
| 15 | A046046 | 15, 30, 45, 60, 75, 95, 110, 125, 140, ... |
| 16 | A046047 | 31, 46, 61, 76, 111, 126, 141, 156, ... |
| 17 | A046048 | 47, 62, 77, 127, 142, 157, 207, 222, ... |
| 18 | A046049 | 63, 78, 143, 158, 223, 238, 303, 318, ... |
| 19 | A046050 | 79, 159, 239, 319, 399 |
The following table gives the numbers which can be represented in 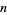 different ways as a sum of
different ways as a sum of 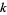 biquadrates.
biquadrates.
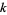 |
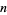 |
OEIS | numbers |
| 1 | 1 | A000583 | 1, 16, 81, 256, 625, 1296, 2401, 4096, ... |
| 2 | 2 | A018786 | 635318657, 3262811042, 8657437697, ... |
The numbers 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 18, 19, 20, 21, ... (OEIS A046039) cannot be represented using distinct biquadrates.
REFERENCES:
Davenport, H. "On Waring's Problem for Fourth Powers." Ann. Math. 40, 731-747, 1939.
Hardy, G. H. and Wright, E. M. "The Representation of a Number by Two or Four Squares." Ch. 20 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 297-316, 1979.
Sloane, N. J. A. Sequences A000583/M5004, A002377, A003336, A003337, A003338, A003339, A003340, A003341, A003342, A003343, A003344, A003345, A003346, A018786, and A046039 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|