
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2019
Date: 14-8-2020
Date: 29-8-2020
|
A number is said to be biquadratefree (or quarticfree) if its prime factorization contains no quadrupled factors. All primes and prime powers 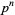 with
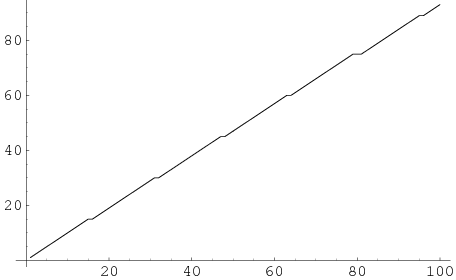
with 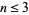 are therefore trivially biquadratefree. The biquadratefree numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, ... (OEIS A046100). The biquadrateful numbers (i.e., those that contain at least one biquadrate) are 16, 32, 48, 64, 80, 81, 96, ... (OEIS A046101). The number of biquadratefree numbers less than 10, 100, 1000, ... are 10, 93, 925, 9240, 92395, 923939, ..., and their asymptotic density is
are therefore trivially biquadratefree. The biquadratefree numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 17, ... (OEIS A046100). The biquadrateful numbers (i.e., those that contain at least one biquadrate) are 16, 32, 48, 64, 80, 81, 96, ... (OEIS A046101). The number of biquadratefree numbers less than 10, 100, 1000, ... are 10, 93, 925, 9240, 92395, 923939, ..., and their asymptotic density is 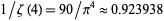 , where
, where 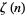 is the Riemann zeta function.
is the Riemann zeta function.
REFERENCES:
Sloane, N. J. A. Sequences A046100 and A046101 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|