


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-12-2019
Date: 4-2-2020
Date: 5-3-2020
|
The conjecture due to Pollock (1850) that every number is the sum of at most five tetrahedral numbers (Dickson 2005, p. 23; incorrectly described as "pyramidal numbers" and incorrectly dated to 1928 in Skiena 1997, p. 43). The conjecture is almost certainly true, but has not yet been proven.
The numbers that are not the sum of 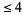 tetrahedral numbers are given by the sequence 17, 27, 33, 52, 73, ..., (OEIS A000797) of 241 terms, with
tetrahedral numbers are given by the sequence 17, 27, 33, 52, 73, ..., (OEIS A000797) of 241 terms, with 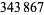 being almost certainly the last such number.
being almost certainly the last such number.
REFERENCES:
Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.
Pollock, F. "On the Extension of the Principle of Fermat's Theorem of the Polygonal Numbers to the Higher Orders of Series Whose Ultimate Differences Are Constant. With a New Theorem Proposed, Applicable to All the Orders." Abs. Papers Commun. Roy. Soc. London 5, 922-924, 1843-1850.
Salzer, H. E. and Levine, N. "Table of Integers Not Exceeding 1000000 that are Not Expressible as the Sum of Four Tetrahedral Numbers." Math. Comput. 12, 141-144, 1958.
Skiena, S. S. The Algorithm Design Manual. New York: Springer-Verlag, pp. 43-45, 1997.
Sloane, N. J. A. Sequence A000797/M5033 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|