MOLECULAR FORCES

One of the most important examples of a non linear restoring force is the molecular force between atoms. Consider, for example, the hydrogen molecule which consists of two hydrogen atoms held together by a molecular force.
In the hydrogen molecule, the hydrogen atoms have an equilibrium separation, and the molecular force provides a restoring force to this equilibrium separation.
The restoring force, however, is quite non linear. If you try to squeeze the atoms together, you quickly build up a large repulsive force that keeps the atoms from penetrating far into each other.
If you try to pull the atoms apart, there is an attractive force that pulls the atoms back together. The attractive force never gets too big, and then dies out when the separation gets much larger than an atomic diameter. In Figure (2) we have sketched the molecular force as a function of the separation of the atoms, the origin being at the equilibrium position. This graph is not too unlike Figure (1) where we have the force curve for the simple pendulum. For the pendulum, the equilibrium position is at θ = 0 , thus the origin of both curves represents the equilibrium position.

Figure 1: The non linear restoring force mg sinθ can be approximated by the straight line (linear term) mg θ if we keep the angle θ small.

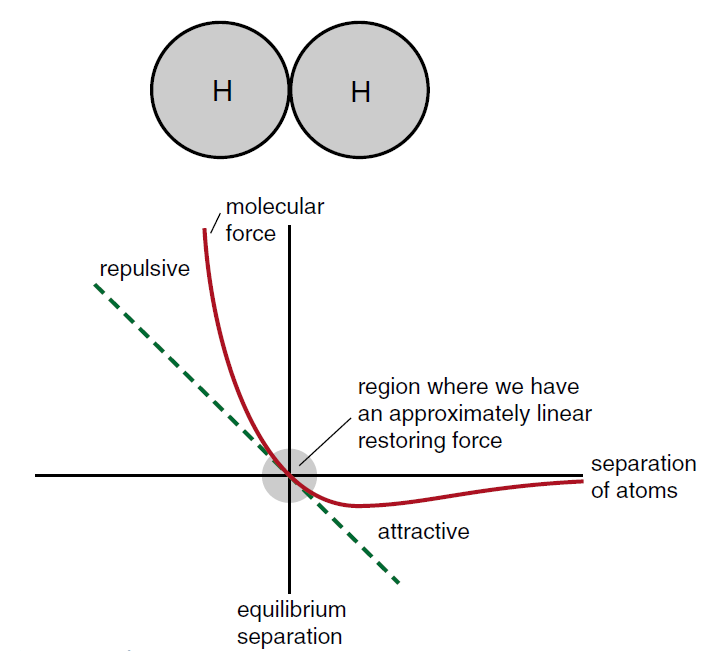
Figure 2: Sketch of the molecular force between two hydrogen atoms. As long as the atoms stay close to the equilibrium position, the force can be represented by a straight line—a linear restoring force.

While the overall shape of the force curves for the simple pendulum and the molecular force are quite different, right in close to the origin both curves can be approximated by a straight line, a linear restoring force.
As long as the amplitudes of the oscillation remain small, we effectively have a linear restoring force and any oscillations should be simple harmonic motion. In Chemistry texts one often sees molecular forces as being represented by springs as shown in Figure (3). The spring force, given by Hooke’s law, is our ideal example of a linear restoring force. We can now see that, while the molecular force in Figure (2) does not look like a linear spring force, if the amplitude of oscillation remains small, the spring force provides a reasonably good approximation to the actual molecular force. The chemist’s diagrams are not so bad after all.
In a crystal, like quartz, where you have many atoms held together by molecular forces, it is possible to get all the atoms oscillating together. Each atom only oscillates a very small distance about its equilibrium position, but all the oscillations can add up to produce a fairly large, quite detectable oscillation of the crystal as a whole. An advantage of a quartz crystal is that these oscillations can be both driven and detected by electric fields. This vibration or simple harmonic motion of a small quartz crystal is used as the basic timing device for digital watches, computers, and almost all forms of modern electronics.
In Galileo’s time we used small oscillations of a non linear harmonic oscillator, the simple pendulum, as a basic time device. Now we use the small oscillations of a non linear harmonic oscillator, the atoms in a quartz crystal, as our most convenient timing device. The main thing we have changed in the last 300 years is not the basic physics, but the size and frequency of the device.

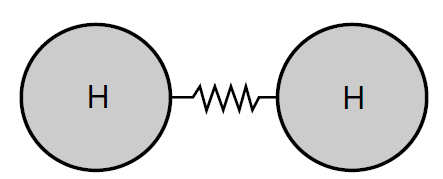
Figure 3: Representation of the molecular force by a spring force.