


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-2-2020
Date: 30-1-2020
Date: 1-12-2019
|
A number 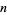 such that
such that
 |
where 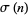 is the divisor function is called a superperfect number. Even superperfect numbers are just
is the divisor function is called a superperfect number. Even superperfect numbers are just 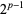 , where
, where 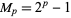 is a Mersenne prime. If any odd superperfect numbers exist, they are square numbers and either
is a Mersenne prime. If any odd superperfect numbers exist, they are square numbers and either 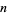 or
or 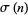 is divisible by at least three distinct primes.
is divisible by at least three distinct primes.
More generally, an 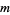 -superperfect (or (
-superperfect (or (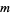 , 2)-superperfect) number is a number for which
, 2)-superperfect) number is a number for which 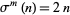 , and an
, and an 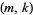 -perfect number is a number
-perfect number is a number 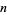 for which
for which 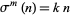 . A number
. A number 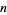 can be tested to see if it is
can be tested to see if it is 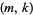 -perfect using the following Wolfram Language code:
-perfect using the following Wolfram Language code:
SuperperfectQ[m_, n_, k_:2] :=
Nest[DivisorSigma[1, #]&, n, m] == k n
The first few (2, 2)-perfect numbers are 2, 4, 16, 64, 4096, 65536, 262144, ... (OEIS A019279; Cohen and te Riele 1996). For 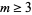 , there are no even
, there are no even 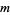 -superperfect numbers (Guy 1994, p. 65). On the basis of computer searches, J. McCranie has shown that there are no
-superperfect numbers (Guy 1994, p. 65). On the basis of computer searches, J. McCranie has shown that there are no 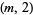 -superperfect numbers less than
-superperfect numbers less than 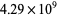 for any
for any 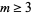 (McCranie, pers. comm., Nov. 11, 2001). McCranie further believes that there are no
(McCranie, pers. comm., Nov. 11, 2001). McCranie further believes that there are no 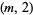 -superperfect numbers for
-superperfect numbers for 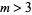 , since
, since 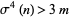 for all
for all 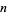 in that range
in that range
REFERENCES:
Cohen, G. L. and te Riele, J. J. "Iterating the Sum-of-Divisors Function." Experim. Math. 5, 93-100, 1996.
Guy, R. K. "Superperfect Numbers." §B9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 65-66, 1994.
Kanold, H.-J. "Über 'Super Perfect Numbers.' " Elem. Math. 24, 61-62, 1969.
Lord, G. "Even Perfect and Superperfect Numbers." Elem. Math. 30, 87-88, 1975.
Sloane, N. J. A. Sequence A019279 in "The On-Line Encyclopedia of Integer Sequences."
Suryanarayana, D. "Super Perfect Numbers." Elem. Math. 24, 16-17, 1969.
Suryanarayana, D. "There Is No Odd Super Perfect Number of the Form 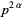 ." Elem. Math. 24, 148-150, 1973.
." Elem. Math. 24, 148-150, 1973.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|