


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-3-2020
Date: 23-8-2020
Date: 8-2-2020
|
Sociable numbers are numbers that result in a periodic aliquot sequence, where an aliquot sequence is the sequence of numbers obtained by repeatedly applying the restricted divisor function
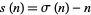 |
(1) |
to 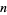 and
and 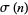 is the usual divisor function.
is the usual divisor function.
If the period of the aliquot cycle is 1, the number is called a perfect number. If the period is 2, the two numbers are called an amicable pair. In general, if the period is 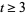 , the number is called sociable of order
, the number is called sociable of order 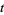 . For example, 1264460 is a sociable number of order four since its aliquot sequence is 1264460, 1547860, 1727636, 1305184, 1264460, ....
. For example, 1264460 is a sociable number of order four since its aliquot sequence is 1264460, 1547860, 1727636, 1305184, 1264460, ....
Only two groups of sociable numbers were known prior to 1970, namely the sets of orders 5 and 28 discovered by Poulet (1918). In 1970, Cohen discovered nine groups of order 4.
The first few sociable numbers are 12496, 14316, 1264460, 2115324, 2784580, 4938136, ... (OEIS A003416), which have orders 5, 28, 4, 4, 4, 4, ... (OEIS A052470). The following table summarizes the smallest members of known social cycles as well as the number of such cycles known (Moews). Excluding perfect numbers, a total of 152 sociable cycles are known as of Feb. 2009 (Pedersen).
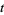 |
OEIS | # | 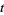 -sociable numbers -sociable numbers |
| 4 | A090615 | 142 | 1264460, 2115324, 2784580, 4938136, 7169104, 18048976, 18656380, ... |
| 5 | 1 | 12496 | |
| 6 | A119478 | 5 | 21548919483, 90632826380, 1771417411016, 3524434872392, 4773123705616 |
| 8 | 2 | 1095447416, 1276254780 | |
| 9 | 1 | 805984760 | |
| 28 | 1 | 14316 |
Y. Kohmoto has considered a generalization of the sociable numbers defined according to the generalized aliquot sequence
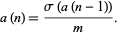 |
(2) |
Multiperfect numbers are fixed points of this mapping, since if 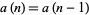 , then
, then
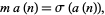 |
(3) |
which is the definition of an 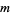 -multiperfect number. If the sequence
-multiperfect number. If the sequence 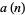 becomes cyclic after
becomes cyclic after 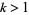 terms, it is then called an
terms, it is then called an  -sociable number of order
-sociable number of order 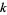 .
.
If 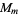 and
and 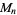 are distinct Mersenne primes, then
are distinct Mersenne primes, then
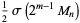 |
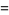 |
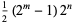 |
(4) |
 |
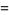 |
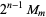 |
(5) |
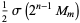 |
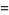 |
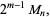 |
(6) |
so 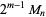 and
and 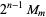 are 1/2-sociable numbers of order 2.
are 1/2-sociable numbers of order 2.
The following table summarizes the smallest members of the generalized 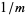 -aliquot sequences of order
-aliquot sequences of order 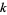 , found by Kohmoto.
, found by Kohmoto.
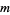 |
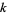 |
starting numbers |
| 3 | 2 | 14913024 |
| 4 | 2 | 2096640, 422688000 |
| 4 | 12 | 3396556800 |
REFERENCES:
Borho, W. "Über die Fixpunkte der 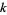 -fach iterierten Teilerersummenfunktion." Mitt. Math. Gesellsch. Hamburg 9, 34-48, 1969.
-fach iterierten Teilerersummenfunktion." Mitt. Math. Gesellsch. Hamburg 9, 34-48, 1969.
Cohen, H. "On Amicable and Sociable Numbers." Math. Comput. 24, 423-429, 1970.
Cohen, G. L. and te Riele, H. J. J. "Iterating the Sum-of-Divisors Function." Amsterdam, Netherlands: Centrum voor Wiskunde en Informatica Report NM-R9525 1995.
Creyaufmüller, W. "Aliquot Sequences." https://www.aliquot.de/aliquote.htm.
Devitt, J. S.; Guy, R. K.; and Selfridge, J. L. Third Report on Aliquot Sequences, Congr. Numer. XVIII, Proc. 6th Manitoba Conf. Numerical Math, pp. 177-204, 1976.
Erdős, P.; Granville, A.; Pomerance, C.; and Spiro, C. "On the Normal Behavior of Iterates of Some Arithmetical Functions." Analytic Number Theory, Proc. Conf. in Honor of P. T. Bateman, Allerton Park, 1989. Boston: Birkhäuser, pp. 165-204, 1990.
Flammenkamp, A. "New Sociable Numbers." Math. Comput. 56, 871-873, 1991.
Gardner, M. "Perfect, Amicable, Sociable." Ch. 12 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 160-171, 1978.
Guy, R. K. "Aliquot Cycles or Sociable Numbers." §B7 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 62-63, 1994.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 145-146, 1979.
Moews, D. "A List of Aliquot Cycles of Length Greater than 2." Rev. Jul. 20, 2005. https://djm.cc/sociable.txt.
Moews, D. "Sociable Numbers." https://djm.cc/amicable.html#sociable.
Moews, D. and Moews, P. C. "A Search for Aliquot Cycles Below 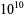 ." Math. Comput. 57, 849-855, 1991.
." Math. Comput. 57, 849-855, 1991.
Moews, D. and Moews, P. C. "A Search for Aliquot Cycles and Amicable Pairs." Math. Comput. 61, 935-938, 1993.
Pedersen, J. A. M. "Tables of Aliquot Cycles." https://amicable.homepage.dk/tables.htm.
Poulet, P. Question 4865. L'interméd. des Math. 25, 100-101, 1918.
Root, S. Item 61 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 23, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/number.html#item61.
Sloane, N. J. A. Sequences A003416, A052470, A090615, and A119478 in "The On-Line Encyclopedia of Integer Sequences."
te Riele, H. J. J. "Perfect Numbers and Aliquot Sequences." In Computational Methods in Number Theory, Part I. (Ed. H. W. Lenstra Jr. and R. Tijdeman). Amsterdam, Netherlands: Mathematisch Centrum, pp. 141-157, 1982.



|
|
|
|
هل يمكن أن تكون الطماطم مفتاح الوقاية من السرطان؟
|
|
|
|
|
|
|
اكتشاف عرائس"غريبة" عمرها 2400 عام على قمة هرم بالسلفادور
|
|
|
|
|
|
|
جامعة الكفيل تقيم ندوة علمية عن الاعتماد الأكاديمي في جامعة جابر بن حيّان
|
|
|