المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Quasiperfect Number |
 670
 05:42 مساءً
date: 29-11-2020 |
Author : Guy, R. K. 
Book or Source : "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory,... 
Page and Part : ...|
Read More
Date: 18-8-2020
1419
Date: 19-2-2020
693
Date: 2-11-2020
695
|
A quasiperfect number, called a "slightly excessive number" by Singh (1997), is a "least" abundant number, i.e., one such that
 |
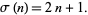Quasiperfect numbers are therefore the sum of their nontrivial divisors. No quasiperfect numbers are known, although if any exist, they must be greater than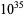 
and have seven or more distinct prime factors (Hagis and Cohen 1982).
REFERENCES:
Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York:Springer-Verlag, pp. 45-53, 1994.
Hagis, P.; and Cohen, G. L. "Some Results Concerning Quasiperfect Numbers." J. Austral. Math. Soc. Ser. A 33, 275-286, 1982.
Singh, S. Fermat's Enigma: The Epic Quest to Solve the World's Greatest Mathematical Problem. New York: Walker, p. 13, 1997.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
