


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-2-2020
Date: 14-3-2020
Date: 14-12-2019
|
A set of positive integers is called weakly triple-free if, for any integer  , the set
, the set 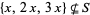 . For example, all subsets of
. For example, all subsets of 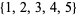 are weakly triple-free except
are weakly triple-free except 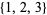 ,
, 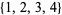 ,
, 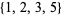 , and
, and 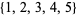 (since each of these contains the subset
(since each of these contains the subset 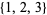 The numbers of weakly triple-free subsets of
The numbers of weakly triple-free subsets of 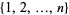 for
for 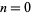 , 1,2, ... are 1, 2, 4, 7, 14, 28, 50, 100, 200, 360, 720, ... (OEIS A068060).
, 1,2, ... are 1, 2, 4, 7, 14, 28, 50, 100, 200, 360, 720, ... (OEIS A068060).
A set of positive integers is called strongly triple-free if 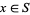 implies
implies 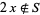 and
and 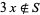 . For example, the only subsets of
. For example, the only subsets of 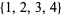 that are strongly triple-free are
that are strongly triple-free are 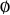 ,
, 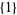 ,
, 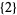 ,
, 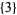 ,
, 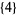 ,
, 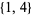 ,
, 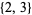 , and
, and 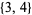 (all other subsets contain either a double or triple of another set element). The numbers of strongly triple-free subsets for
(all other subsets contain either a double or triple of another set element). The numbers of strongly triple-free subsets for 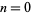 , 1, 2, ... are 1, 2, 3, 5, 8, 16, 24, 48, 76, 132, ... (OEIS A050295).
, 1, 2, ... are 1, 2, 3, 5, 8, 16, 24, 48, 76, 132, ... (OEIS A050295).
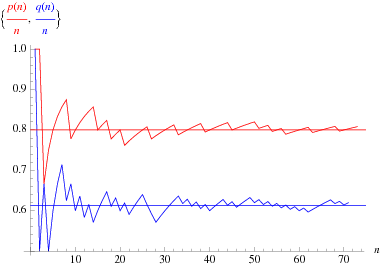
Define
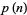 |
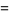 |
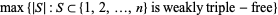 |
(1) |
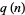 |
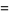 |
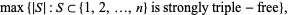 |
(2) |
where 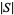 denotes the cardinal number of (number of members in)
denotes the cardinal number of (number of members in) 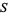 . Then for
. Then for 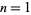 , 2, ...,
, 2, ..., 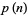 is given by 1, 2, 2, 3, 4, 4, 5, 6, 7, 8, 9, 9, 10, 11, 11, ... (OEIS A157282), and
is given by 1, 2, 2, 3, 4, 4, 5, 6, 7, 8, 9, 9, 10, 11, 11, ... (OEIS A157282), and 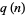 by 1, 1, 2, 2, 3, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, ... (OEIS A050296). Asymptotic formulas are given by
by 1, 1, 2, 2, 3, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, ... (OEIS A050296). Asymptotic formulas are given by
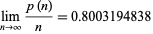 |
(3) |
(conjectured) and
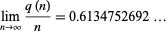 |
(4) |
(OEIS A086316; Finch 2003).
REFERENCES:
Chung, F.; Erdős, P.; and Graham, R. "On Sparse Sets Hitting Linear Forms." In Number Theory for the Millennium, vol. 1, Proc. 2000 Urbana Conf. (Ed. M. A. Bennett, B. C. Berndt, N. Boston, H. G. Diamond, A. J. Hildebrand, and W. Philipp). Natick, MA: A K Peters, pp. 257-272, 2002.
Finch, S. "Triple-Free Sets of Integers." Sep. 5, 2002. https://algo.inria.fr/csolve/triple/.
Finch, S. R. "Triple-Free Set Constants." §2.26 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 183-185, 2003.
Graham, R.; Spencer, J.; and Witsenhausen, H. "On Extremal Density Theorems for Linear Forms." In Number Theory and Algebra (Ed. H. Zassenhaus). New York: Academic Press, pp. 103-109, 1977.
Reznick, B. and Holzsager, R. "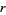 -fold Free Sets of Positive Integers." Math. Mag. 68, 71-72, 1995.
-fold Free Sets of Positive Integers." Math. Mag. 68, 71-72, 1995.
Sloane, N. J. A. Sequences A050295, A050296, A068060, A086316, and A157282 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|