
Dickman Function
 المؤلف:
Dickman, K.
المؤلف:
Dickman, K.
 المصدر:
"On the Frequency of Numbers Containing Prime Factors of a Certain Relative Magnitude." Arkiv för Mat., Astron. och Fys. 22A
المصدر:
"On the Frequency of Numbers Containing Prime Factors of a Certain Relative Magnitude." Arkiv för Mat., Astron. och Fys. 22A
 الجزء والصفحة:
...
الجزء والصفحة:
...
 14-3-2020
14-3-2020
 2268
2268
Dickman Function
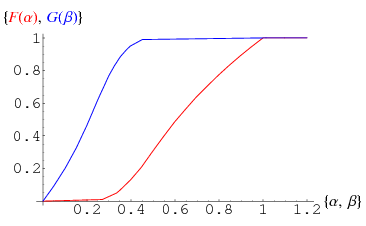
The probability that a random integer between 1 and  will have its greatest prime factor
will have its greatest prime factor 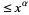 approaches a limiting value
approaches a limiting value  as
as  , where
, where 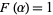 for
for 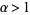 and
and 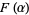 is defined through the integral equation
is defined through the integral equation
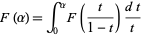 |
(1)
|
for 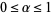 (Dickman 1930, Knuth 1998), which is almost (but not quite) a homogeneous Volterra integral equation of the second kind. The function can be given analytically for
(Dickman 1930, Knuth 1998), which is almost (but not quite) a homogeneous Volterra integral equation of the second kind. The function can be given analytically for 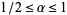 by
by
(Knuth 1998).
Amazingly, the average value of  such that
such that 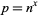 is
is
which is precisely the Golomb-Dickman constant 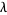 , which is defined in a completely different way!
, which is defined in a completely different way!
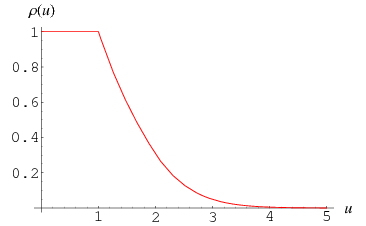
The Dickman function can be solved numerically by converting it to a delay differential equation. This can be done by noting that 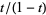 will become
will become 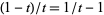 upon multiplicative inversion, so define
upon multiplicative inversion, so define 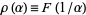 to obtain
to obtain
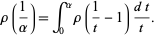 |
(10)
|
Now change variables under the integral sign by defining
so
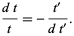 |
(13)
|
Plugging back in gives
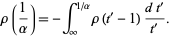 |
(14)
|
To get rid of the 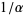 s, define
s, define 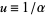 , so
, so
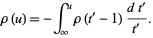 |
(15)
|
But by the first fundamental theorem of calculus,
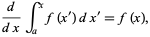 |
(16)
|
so differentiating both sides of equation (15) gives
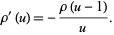 |
(17)
|
This holds for 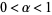 , which corresponds to
, which corresponds to 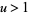 . Rearranging and combining with an appropriate statement of the condition
. Rearranging and combining with an appropriate statement of the condition 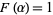 for
for 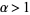 in the new variables then gives
in the new variables then gives
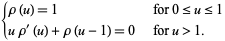 |
(18)
|
The second-largest prime factor will be 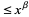 is given by an expression similar to that for
is given by an expression similar to that for 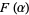 . It is denoted
. It is denoted 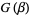 , where
, where 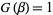 for
for 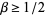 and
and
/t](https://mathworld.wolfram.com/images/equations/DickmanFunction/NumberedEquation9.gif) |
(19)
|
for 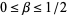 .
.
REFERENCES:
Dickman, K. "On the Frequency of Numbers Containing Prime Factors of a Certain Relative Magnitude." Arkiv för Mat., Astron. och Fys. 22A, 1-14, 1930.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 382-384, 1998.
Norton, K. K. Numbers with Small Prime Factors, and the Least kth Power Non-Residue. Providence, RI: Amer. Math. Soc., 1971.
Panario, D. "Smallest Components in Combinatorial Structures." Feb. 16, 1998. http://algo.inria.fr/seminars/sem97-98/panario.pdf.
Ramaswami, V. "On the Number of Positive Integers Less than  and Free of Prime Divisors Greater than
and Free of Prime Divisors Greater than 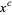 ." Bull. Amer. Math. Soc. 55, 1122-1127, 1949.
." Bull. Amer. Math. Soc. 55, 1122-1127, 1949.
Ramaswami, V. "The Number of Positive Integers 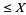 and Free of Prime Divisors
and Free of Prime Divisors 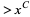 , and a Problem of S. S. Pillai." Duke Math. J. 16, 99-109, 1949.
, and a Problem of S. S. Pillai." Duke Math. J. 16, 99-109, 1949.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


