تقريب الذرات المنفصلة Separated Atoms

في الحالة المحددة ∞→R كل حالة جزيئية تحصل على مزيج من الحالات المعروفة للذرتين فمسقط L_A على محور z M_L)_Ah) ومسقط L_B على محور  M_L)_Bh).

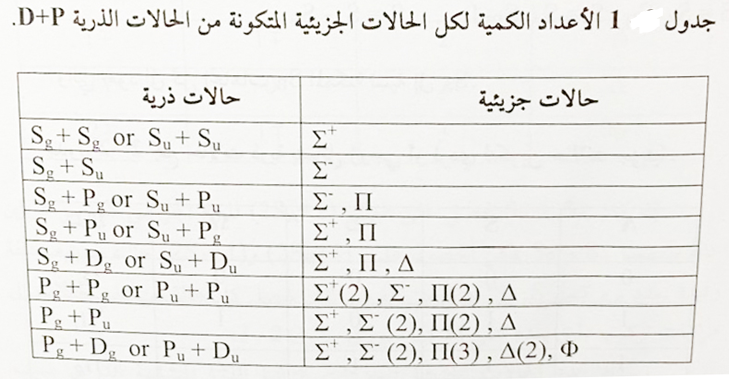
ويتكون منهما العدد الكمي الجزيئي 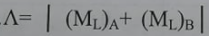ياخذ M_L القيم من –L والى L ولذلك ينتج عدد كبير من قيم Λ لمجموعة معينة من قيم L_A وL_B ويكون عدد الحالات الالكترونية الجزيئية اكبر بكثير من عدد الحالات الالكترونية للذرتين المشاركتين في تكوين الجزيئة وفي الجدول 1 مبين كل الحالات الالكترونية الممكنة التي تظهر من مزج الذرية D وفيها L_A=2 مع الحالة الذرية وفيها L_B=2.

خواص التماثل للحالات الجزيئية تشتق من الحالات الذرية للذرةA  وللذرة B. تملك الحالة الذرية تماثل زوجي اذا كان الجمع Σl_i على اعداد الزخم الزاوي المداري لجميع الالكترونات زوجي، ويكون التماثل فردي اذا كان الجمع فردي. في الجدول 2 مبين تماثلات الحالات الجزيئية المشتقة من عدد من الحالات الذرية.

لبرم الحالات الذرية S_A وS_B تاثير في تكوين الحالات الجزيئية. البرم الجزيئي الناتج يساوي S=S_A+S_B ومقداره 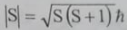واذا كان S_B < S_A فان عدد البرم الكمي S ياخذ القيم (2S_B+1):

والتي تعود الى كل اتجاهات S_B الممكنة نسبة الى S_A.

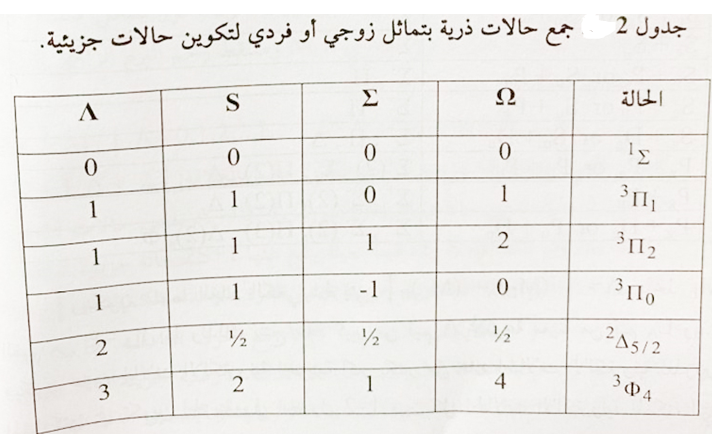
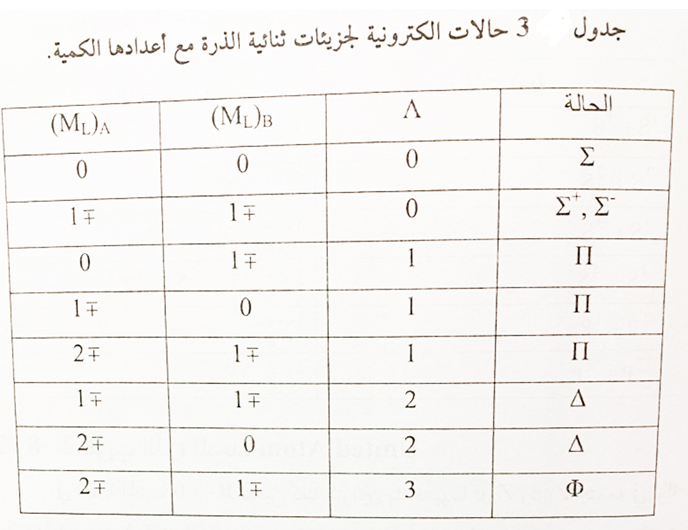
اذا كان S_B ≥ S_A نحصل على القيم (2S_A+1) للبرم الجزيئي S. من ذرتين حالة برمهما S_A وS_B يمكن لحصول على (2S_B+1) و(2S_A+1) حالة جزيئية مختلفة ومميزة بعدد برم كمي S. الازدواج بين البرم والمدار يفصل كل حالة من هذه الحالات الى مركبات تركيب دقيق بعدد كمي Ω كما مبين في جدول 3.

ويزداد عدد الحالات الجزيئية الثنائية الذرة المتشابهة الذرتين بسبب خاصية التماثل الاضافية فكل حالة يمكن تصنيفها الى زوجية تماثل الدالة الموجية او فردية تماثل الدالة الموجية، وفي الجدول 4 مبين كل الحالات الجزيئية المتكونة من ذرتين متشابهتين وفي نفس الحالة الذرية.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يقيم مسابقة الكوثر الخاصة بترتيل القرآن الكريم في كربلاء

قسم الشؤون الفكرية والثقافية يُصدر العدد الثالث والعشرين من مجلّة (أوراق معرفية)

قسم التربية والتعليم يُطلق الموسم التدريبيّ الصيفيّ لملاكات مجموعة العميد التربوية

المجمَع العلمي يُطلق المرحلة الثالثة من مشروع أمير القرّاء الوطني

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon