


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-5-2020
Date: 16-8-2020
Date: 7-3-2020
|
An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity
![O{exp[c(logn)^(1/3)(loglogn)^(2/3)]},](https://mathworld.wolfram.com/images/equations/NumberFieldSieve/NumberedEquation1.gif) |
(1) |
reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of 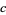 relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers near a large power,
relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers near a large power,
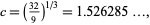 |
(2) |
for the "general" case applicable to any odd positive number which is not a power,
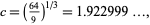 |
(3) |
and for a version using many polynomials (Coppersmith 1993),
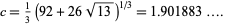 |
(4) |
REFERENCES:
Coppersmith, D. "Modifications to the Number Field Sieve." J. Cryptology 6, 169-180, 1993.
Coppersmith, D.; Odlyzko, A. M.; and Schroeppel, R. "Discrete Logarithms in GF(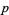 )." Algorithmics 1, 1-15, 1986.
)." Algorithmics 1, 1-15, 1986.
Cowie, J.; Dodson, B.; Elkenbracht-Huizing, R. M.; Lenstra, A. K.; Montgomery, P. L.; Zayer, J. A. "World Wide Number Field Sieve Factoring Record: On to 512 Bits." In Advances in Cryptology--ASIACRYPT '96 (Kyongju) (Ed. K. Kim and T. Matsumoto.) New York: Springer-Verlag, pp. 382-394, 1996.
Elkenbracht-Huizing, R.-M. "A Multiple Polynomial General Number Field Sieve." Algorithmic Number Theory (Talence, 1996). New York: Springer-Verlag, pp. 99-114, 1996.
Elkenbracht-Huizing, R.-M. "An Implementation of the Number Field Sieve." Experiment. Math. 5, 231-253, 1996.
Elkenbracht-Huizing, R.-M. "Historical Background of the Number Field Sieve Factoring Method." Nieuw Arch. Wisk. 14, 375-389, 1996.
Elkenbracht-Huizing, R.-M. Factoring Integers with the Number Field Sieve. Doctor's Thesis, Leiden University, 1997.
Lenstra, A. K. and Lenstra, H. W. Jr. "Algorithms in Number Theory." In Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity (Ed. J. van Leeuwen). New York: Elsevier, pp. 673-715, 1990.
Lenstra, A. K. and Lenstra, H. W. Jr. The Development of the Number Field Sieve. Berlin: Springer-Verlag, 1993.
Pomerance, C. "A Tale of Two Sieves." Not. Amer. Math. Soc. 43, 1473-1485, 1996.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
جامعة الفلوجة: حفل تخرج طلبة الجامعات يهدف إلى جمع الطلبة تحت خيمة العراق الموحد
|
|
|