The conjecture made by Belgian mathematician Eugène Charles Catalan in 1844 that 8 and 9 (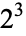 and 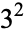) are the only consecutive powers (excluding 0 and 1). In other words,

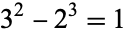(1)

is the only nontrivial solution to Catalan's Diophantine problem

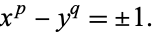(2)

The special case 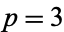 and 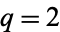 is the  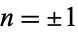case of a Mordell curve.

Interestingly, more than 500 years before Catalan formulated his conjecture, Levi ben Gerson (1288-1344) had already noted that the only powers of 2 and 3 that apparently differed by 1 were 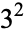 and 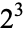 (Peterson 2000).

This conjecture had defied all attempts to prove it for more than 150 years, although Hyyrő and Makowski proved that no three consecutive powers exist (Ribenboim 1996), and it was also known that 8 and 9 are the only consecutive cubic and square numbers (in either order). Finally, on April 18, 2002, Mihăilescu sent a manuscript proving the entire conjecture to several mathematicians (van der Poorten 2002). The proof has now appeared in print (Mihăilescu 2004) and is widely accepted as being correct and valid (Daems 2003, Metsänkylä 2003).

Tijdeman (1976) showed that there can be only a finite number of exceptions should the conjecture not hold. More recent progress showed the problem to be decidable in a finite (but more than astronomical) number of steps and that, in particular, if 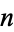 and 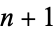 are powers, then  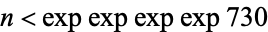(Guy 1994, p. 155). In 1999, M. Mignotte showed that if a nontrivial solution exists, then 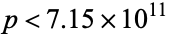,  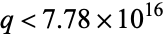(Peterson 2000).

It had also been known that if additional solutions to the equation exist, either the exponents 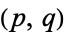 must be double Wieferich prime pairs, or  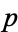and 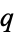 must satisfy a class number divisibility condition (Steiner 1998). Constraints on this class number condition were continuously improved starting with Inkeri (1964) and continuing through the work of Steiner (1998). Then, in the spring of 1999, Bugeaud and Hanrot proved the weakest possible class number condition holds unconditionally (i.e., irrespective of whether  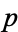and 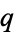 are a double Wieferich prime pair or not). Subsequently, in Autumn 2000, Mihailescu proved that the double Wieferich prime pair condition also must hold unconditionally (Peterson 2000).

A generalization to Gaussian integers that differ by a unit is given by

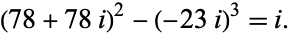(3)

REFERENCES:

Bilu, Y. F. "Catalan's Conjecture (After Mihăilescu)." Astérisque, No. 294, 1-26, 2004.

Bilu, Y. F. "Catalan Without Logarithmic Forms (after Bugeaud, Hanrot and Mihăilescu)." J. Théor. Nombres Bordeaux 17, 69-85, 2005.

Catalan, E. "Note extraite d'une lettre adressée à l'éditeur." J. reine angew. Math. 27, 192, 1844.

Daems, J. "A Cyclotomic Proof of Catalan's Conjecture." Sept. 29, 2003. https://www.math.leidenuniv.nl/~jdaems/scriptie/Catalan.pdf.

Guy, R. K. "Difference of Two Power." §D9 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 155-157, 1994.

Inkeri, K. "On Catalan's Problem." Acta Arith. 9, 285-290, 1964.

Metsänkylä, T. "Catalan's Conjecture: Another Old Diophantine Problem Solved." Bull. Amer. Math. Soc. 41, 43-57, 2003.

Mihăilescu, P. "A Class Number Free Criterion for Catalan's Conjecture." J. Number Th. 99, 225-231, 2003.

Mihăilescu, P. "Primary Cyclotomic Units and a Proof of Catalan's Conjecture." J. reine angew. Math. 572, 167-195, 2004.

Peterson, I. "MathTrek: Zeroing In on Catalan's Conjecture." Dec. 4, 2000. https://www.sciencenews.org/20001202/mathtrek.asp.

Ribenboim, P. "Consecutive Powers." Expositiones Mathematicae 2, 193-221, 1984.

Ribenboim, P. Catalan's Conjecture: Are 8 and 9 the only Consecutive Powers? Boston, MA: Academic Press, 1994.

Ribenboim, P. "Catalan's Conjecture." Amer. Math. Monthly 103, 529-538, 1996.

Steiner, R. "Class Number Bounds and Catalan's Equation." Math. Comput. 67, 1317-1322, 1998.

Tijdeman, R. "On the Equation of Catalan." Acta Arith. 29, 197-209, 1976.

van der Poorten, A. "Concerning: Catalan's Conjecture Proved?." 5 May 2002. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0205&L=nmbrthry&P=269.

Weisstein, E. W. "Draft Proof of Catalan's Conjecture Circulated." MathWorld Headline News, May 5, 2002. https://mathworld.wolfram.com/news/2002-05-05/catalan/.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 71 and 73, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة: نهج البلاغة مصدر صافٍ للفكر والمعرفة ومحصِّنٌ من الشبهات

العتبة العباسية المقدسة تطلق محاضرات محفل نهج البلاغة الأسبوعي في ذي قار

العتبتان المقدستان الحسينية والعباسية تدعوان للمشاركة في مهرجان الشموع بنسخته السادسة والعشرين

بالتعاون مع مستشفى الكفيل.. قسم الشؤون الطبّية يواصل إقامة البرنامج التدريبي لملاكاته النسوية

المزيد

الآخبار الصحية

الصحة العالمية تكشف حقيقة انتشار فيروس نيباه خارج الهند

متى يصبح محيط الخصر "مؤشر خطر"؟

دراسة تكشف دور "العوامل الوراثية" في تحديد عمر الإنسان

رائحة كريهة في الجسم.. "علامة خفية" أخطر مما تتصور

المزيد

الآخبار التكنلوجية

مايكروسوفت تكشف عن الجيل الثاني من شرائحها للذكاء الاصطناعي

خرافة "ثمانية أكواب يوميا".. كم من الماء يحتاج جسمك فعليا؟

هل توجد حياة خارج كوكبنا؟.. اكتشاف جديد يثير اهتمام العلماء

اكتشاف الخلايا المسؤولة عن فقدان ذاكرة الطفولة

المزيد