


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2020
Date: 9-3-2020
Date: 13-2-2020
|
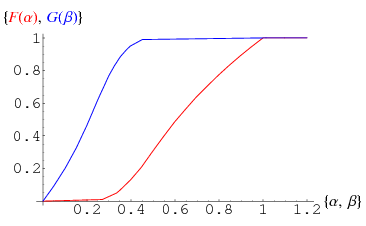
The probability that a random integer between 1 and  will have its greatest prime factor
will have its greatest prime factor 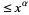 approaches a limiting value
approaches a limiting value 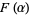 as
as 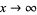 , where
, where 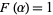 for
for 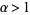 and
and 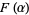 is defined through the integral equation
is defined through the integral equation
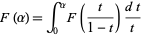 |
(1) |
for 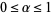 (Dickman 1930, Knuth 1998), which is almost (but not quite) a homogeneous Volterra integral equation of the second kind. The function can be given analytically for
(Dickman 1930, Knuth 1998), which is almost (but not quite) a homogeneous Volterra integral equation of the second kind. The function can be given analytically for 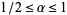 by
by
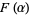 |
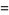 |
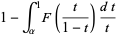 |
(2) |
 |
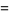 |
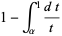 |
(3) |
 |
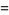 |
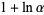 |
(4) |
(Knuth 1998).
Amazingly, the average value of  such that
such that 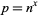 is
is
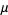 |
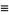 |
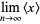 |
(5) |
 |
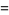 |
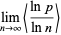 |
(6) |
 |
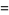 |
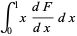 |
(7) |
 |
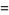 |
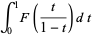 |
(8) |
 |
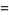 |
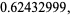 |
(9) |
which is precisely the Golomb-Dickman constant 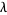 , which is defined in a completely different way!
, which is defined in a completely different way!
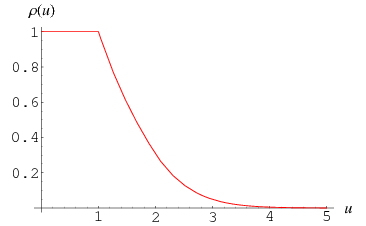
The Dickman function can be solved numerically by converting it to a delay differential equation. This can be done by noting that 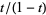 will become
will become 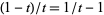 upon multiplicative inversion, so define
upon multiplicative inversion, so define 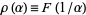 to obtain
to obtain
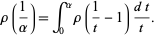 |
(10) |
Now change variables under the integral sign by defining
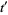 |
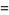 |
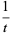 |
(11) |
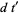 |
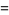 |
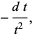 |
(12) |
so
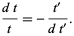 |
(13) |
Plugging back in gives
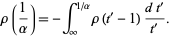 |
(14) |
To get rid of the 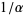 s, define
s, define 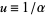 , so
, so
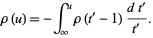 |
(15) |
But by the first fundamental theorem of calculus,
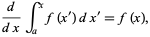 |
(16) |
so differentiating both sides of equation (15) gives
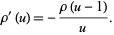 |
(17) |
This holds for 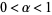 , which corresponds to
, which corresponds to 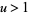 . Rearranging and combining with an appropriate statement of the condition
. Rearranging and combining with an appropriate statement of the condition 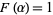 for
for 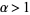 in the new variables then gives
in the new variables then gives
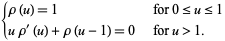 |
(18) |
The second-largest prime factor will be 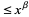 is given by an expression similar to that for
is given by an expression similar to that for 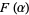 . It is denoted
. It is denoted 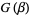 , where
, where 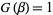 for
for 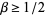 and
and
/t](https://mathworld.wolfram.com/images/equations/DickmanFunction/NumberedEquation9.gif) |
(19) |
for 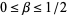 .
.
REFERENCES:
Dickman, K. "On the Frequency of Numbers Containing Prime Factors of a Certain Relative Magnitude." Arkiv för Mat., Astron. och Fys. 22A, 1-14, 1930.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 382-384, 1998.
Norton, K. K. Numbers with Small Prime Factors, and the Least kth Power Non-Residue. Providence, RI: Amer. Math. Soc., 1971.
Panario, D. "Smallest Components in Combinatorial Structures." Feb. 16, 1998. https://algo.inria.fr/seminars/sem97-98/panario.pdf.
Ramaswami, V. "On the Number of Positive Integers Less than  and Free of Prime Divisors Greater than
and Free of Prime Divisors Greater than 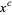 ." Bull. Amer. Math. Soc. 55, 1122-1127, 1949.
." Bull. Amer. Math. Soc. 55, 1122-1127, 1949.
Ramaswami, V. "The Number of Positive Integers 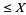 and Free of Prime Divisors
and Free of Prime Divisors 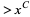 , and a Problem of S. S. Pillai." Duke Math. J. 16, 99-109, 1949.
, and a Problem of S. S. Pillai." Duke Math. J. 16, 99-109, 1949.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|