Lehmer's Totient Problem

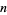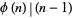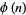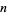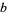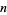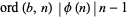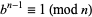Lehmer's totient problem asks if there exist any composite numbers  such that , where  is the totient function? No such numbers are known. However, any such an  would need to be a Carmichael number, since for every element  in the integers (mod ), , so  and 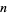 is a Carmichael number.

In 1932, Lehmer showed that such an 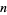 must be odd and squarefree, and that the number of distinct prime factors  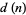must satisfy 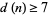. This was subsequently extended to 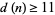. The best current result is  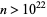and 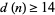, improving the  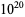lower bound of Cohen and Hagis (1980) since there are no Carmichael numbers less than  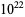having  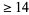distinct prime factors; Pinch). However, even better results are known in the special cases 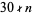, in which case  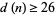(Wall 1980), and 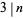, in which case  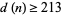and 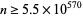 (Lieuwens 1970).

REFERENCES:

Cohen, G. L. and Hagis, P. Jr. "On the Number of Prime Factors of 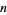 is 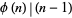." Nieuw Arch. Wisk. 28, 177-185, 1980.

Cohen, G. L. and Segal, S. L. "A Note Concerning Those 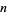 for which  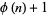Divides 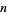." Fib. Quart. 27, 285-286, 1989.

Lieuwens, E. "Do There Exist Composite Numbers for Which 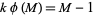 Holds?" Nieuw Arch. Wisk. 18, 165-169, 1970.

Pinch, R. G. E. ftp://ftp.dpmms.cam.ac.uk/pub/Carmichael/table.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 27-28, 1989.

Wall, D. W. "Conditions for 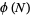 to Properly Divide 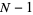." In A Collection of Manuscripts Related to the Fibonacci Sequence (Ed. V. E. Hoggatt and M. V. E. Bicknell-Johnson). San Jose, CA: Fibonacci Assoc., pp. 205-208, 1980.