Magnification limits
 

There are both lower and upper limits to the magnification which can be usefully applied with any given telescope. The first consideration for a lower limit is that all the light which is collected by the telescope should be made available for viewing by the eye; the magnification must be sufficiently great to make the exit pupil equal to or smaller than the entrance pupil of the eye (see figure 17.2).

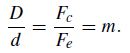(1)

Thus, byusing the definition of magnification given by equation (1), this condition can be written as
m ≥ D/d
where d is the diameter of the pupil of the eye and D the diameter of the telescope aperture. Under normal observing conditions, a typical value of d is 8 mm and, thus, the lower limit of magnification is set by
m ≥ D/8 (2)
where the diameter of the telescope is again expressed in mm. If the magnification is less than the value given by equation (2), some light will be lost and the full collecting power of the telescope is not being utilized. This consideration is very important, except perhaps when the Moon is being viewed.
A further lower limit to the magnification is set by the resolving power of the eye. If any detail in a complex object is to be viewed, the angular size of its image must be larger than the eye’s resolving power. This latter quantity depends, to a great extent, on the observer but a typical value can be taken as one minute of arc. If a certain resolution has been achieved by using a particular telescope, the magnification must have a value which is sufficient to allow the resolved details to be seen by eye. Thus, by matching the resolution of the telescope to that of the eye (≈ 60 arc seconds) by means of magnification, a lower limit of magnification is set by
m ≥ 60D/140
or
m ≥ 3D/7.
As the value taken for the resolving power of the eye favours an extremely good eye, the lower limit of magnification can be conveniently approximated to
m ≥ D/2 (3)
where the diameter of the telescope, D, is again expressed in mm.
The useful magnification of a telescope cannot be increased indefinitely. The upper limit is set by the impracticability of making eyepieces with extremely short focal lengths, by the quality of the optics of the collector and by the fact that the ability of the eye to record good images deteriorates when the beam that it accepts becomes too small. For the image to be seen without loss in the quality of the eye’s function, the exit pupil must be larger than 0·8 mm. By using equation (1) for the expression defining magnification,
m ≤ D/0·8 (4)
where, again, the diameter of the telescope is in mm. Comparison of equations (2) and (4) shows that from a consideration of the size of exit pupil, the magnifying power of any telescope has a useful range covered by a factor of ten. According to an empirical relation known as Whittaker’s rule, deterioration of a viewed image sets in when the value of magnification exceeds the diameter of the telescope, D, expressed in mm. Using this rule, m ≤ D.
The lower and upper limits discussed earlier do not pretend to be hard and fast rules but serve only as guides. The limits of magnification also depend on the type of object that is being viewed. It may be possible, for example, to use a magnification given by 2D when the object is a double star. Magnifications greater than D (Whittaker’s rule) can be used occasionally, especially with telescopes of small aperture. In fact, it has been found that in the case of double star observations with telescopes of small-to-medium aperture, the upper limit for magnification does not have a linear relationship with the telescope’s diameter. According to Lewis, the upper limit is given by
(5)
Inspection of equation (5) shows that for telescopes of small aperture, magnifications close to 2D can be used but for medium-sized telescopes, the upper limit of magnification is reduced to values which are closer to D. The nonlinear dependence of the upper limit of magnification on the aperture of the telescope probably results from the way in which the telescope image is distorted by the seeing effects of the Earth’s atmosphere. The appearance of an image distorted by seeing conditions depends on the aperture of the telescope . In many cases, the upper limit of magnification is set by the seeing conditions and these vary greatly from site to site and from night to night.