


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-6-2020
Date: 16-8-2020
Date: 11-11-2020
|
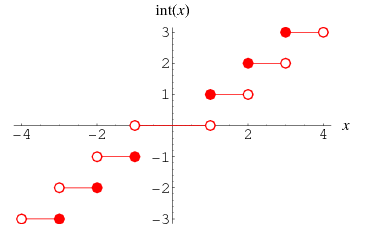
The function 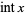 gives the integer part of
gives the integer part of  . In many computer languages, the function is denoted int(x). It is related to the floor and ceiling functions
. In many computer languages, the function is denoted int(x). It is related to the floor and ceiling functions 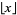 and
and ![[x]](https://mathworld.wolfram.com/images/equations/IntegerPart/Inline4.gif) by
by
![int(x)={|_x_| for x>=0; [x] for x<0.](https://mathworld.wolfram.com/images/equations/IntegerPart/NumberedEquation1.gif) |
(1) |
The integer part function satisfies
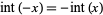 |
(2) |
and is implemented in the Wolfram Language as IntegerPart[x]. This definition is chosen so that 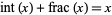 , where
, where 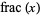 is the fractional part. Although Spanier and Oldham (1987) use the same definition as in the Wolfram Language, they mention the formula only very briefly and then say it will not be used further. Graham et al. (1994), and perhaps most other mathematicians, use the term "integer" part interchangeably with the floor function
is the fractional part. Although Spanier and Oldham (1987) use the same definition as in the Wolfram Language, they mention the formula only very briefly and then say it will not be used further. Graham et al. (1994), and perhaps most other mathematicians, use the term "integer" part interchangeably with the floor function 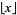 .
.
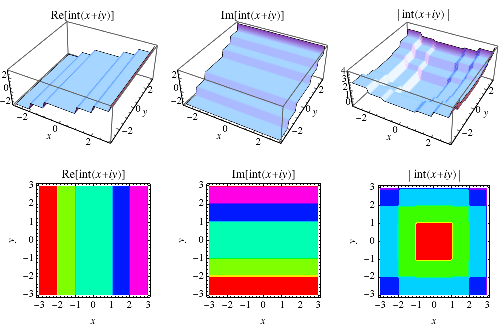 |
The integer part function can also be extended to the complex plane, as illustrated above.
Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).
| notation | name | S&O | Graham et al. | Wolfram Language |
![[x]](https://mathworld.wolfram.com/images/equations/IntegerPart/Inline8.gif) |
ceiling function | -- | ceiling, least integer | Ceiling[x] |
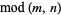 |
congruence | -- | -- | Mod[m, n] |
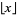 |
floor function | 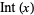 |
floor, greatest integer, integer part | Floor[x] |
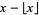 |
fractional value | 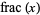 |
fractional part or 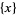 |
SawtoothWave[x] |
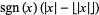 |
fractional part | 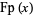 |
no name | FractionalPart[x] |
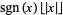 |
integer part | 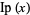 |
no name | IntegerPart[x] |
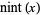 |
nearest integer function | -- | -- | Round[x] |
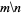 |
quotient | -- | -- | Quotient[m, n] |
REFERENCES:
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 67, 1994.
Spanier, J. and Oldham, K. B. "The Integer-Value Int( ) and Fractional-Value frac(
) and Fractional-Value frac( ) Functions." Ch. 9 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 71-78, 1987.
) Functions." Ch. 9 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 71-78, 1987.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|