Newton’s form of Kepler’s third law
المؤلف:
A. Roy, D. Clarke
المصدر:
Astronomy - Principles and Practice 4th ed
الجزء والصفحة:
p 179
11-8-2020
1881
Newton’s form of Kepler’s third law
Let two planets revolve about the Sun in orbits of semi-major axes a1 and a2, with periods of revolution T1 and T2. Let the masses of the Sun and the two planets be M, m1 and m2 respectively.
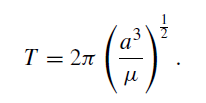(1)
Then by equation (1),
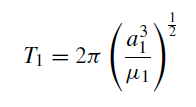
where μ1 = G(M + m1). Also,
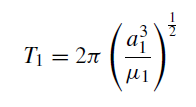
Hence,
(2)
Kepler’s third law would have been written as
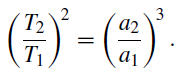
The only difference between this last equation and (2) is a factor k, where
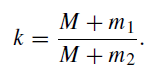
Dividing top and bottom by M, we obtain
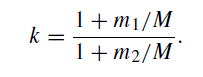
The greatest departure of k from unity arises when we take the two planets to be the most massive and the least massive in the Solar System. The most massive is Jupiter: in this case m1/M = 1/1047·3. Of the planets known to Newton, the least massive was Mercury, giving m2/M = 1/6 200 000. Hence, to three significant figures, k = 1. Kepler’s third law is, therefore, only an approximation to the truth, though a very good one. Newton’s form of Kepler’s third law, namely equation (2), is much better.
الاكثر قراءة في مواضيع عامة في علم الفلك
اخر الاخبار
اخبار العتبة العباسية المقدسة
