The geocentric celestial sphere
 

So far we have assumed that the celestial sphere is centred at the observer. In the case of measurements made in the alt-azimuth system of coordinates, we have seen that as altitude and azimuth are linked to an observer’s latitude and longitude, there are as many pairs of coordinates for a star’s position at a given time as there are observers, even though the size of the Earth is vanishingly small compared with stellar distances.
Even in the equatorial system, the multitude of observing positions scattered over the Earth raises problems. For example, let us consider the declination of a star. To the observer at O (see figure 1), the direction of the north celestial pole OP' is parallel to the direction CP in which it would be seen from the Earth’s centre. Likewise the plane of the celestial equator DOB is parallel to the celestial equator obtained by extending in the Earth’s equatorial plane FCA to cut the celestial sphere. A star’s direction, as observed from O, would also be parallel to its direction as observed from C. Thus, OM' is parallel to CM where OM' is the direction to a particular star. So far, no problem is raised: the star’s declination, δ', as measured at O, is ∠BOM', equal to the geocentric declination, δ, or ∠ACM.

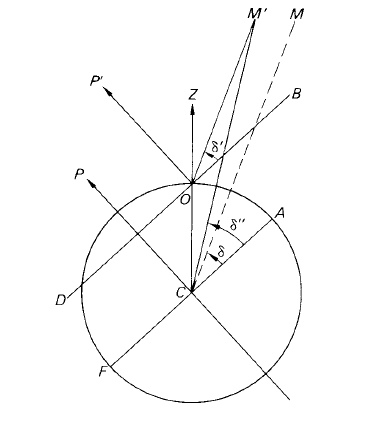
Figure 1. The geocentric celestial sphere showing the effect of parallax by moving the centre of a celestial sphere from an observer to the centre of the Earth.

There are a number of celestial objects, however, where a problem does arise. These objects are within the Solar System—for example, the Sun, the planets and their satellites, comets and meteors and, of course, artificial satellites and other spacecraft. None of these can be considered to be at an infinite distance. A shift in the observer’s position from O to C, therefore, causes an apparent shift in their positions on the celestial sphere. We call such a movement (due, in fact, to a shift in the observer’s position) a parallactic shift. Obviously, this apparent angular shift will be the greater, the closer the object is to the Earth. In particular, if M' is such an object, its declination, δ', given by ∠BOM' will no longer be equal to its geocentric declination, δ'', given by ∠ACM'. In passing, it may be mentioned that ∠OM'C is called the parallactic angle.

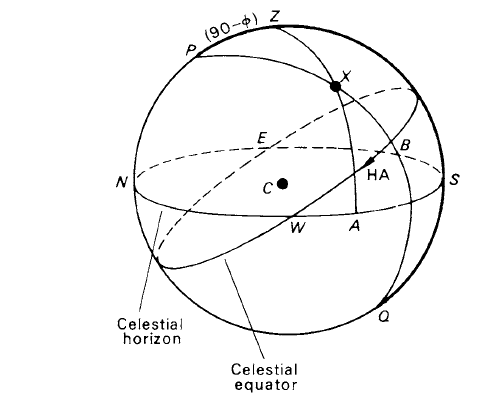
Figure 2. The geocentric celestial sphere and the position of a star.
 

In the almanacs such as The Astronomical Almanac, information about the positions of celestial objects, including the planets, is given for various dates throughout the year. It would be impossible to tabulate the declinations of a planet at a particular date for all possible observers. Hence, such information is tabulated for a hypothetical observer stationed at the Earth’s centre. Various correction procedures are available so that any observer can convert the tabulated geocentric data to topocentric (or local) data.
 

From now on, unless otherwise stated, we will consider any celestial sphere to be a standard geocentric one. Thus, in figure 2. we have a geocentric celestial sphere for an observer in latitude ∅ N. The zenith is obtained by drawing a straight line from the Earth’s centre through the observer on the Earth’s surface to intersect the celestial sphere at Z. The celestial horizon NWSE is the great circle with Z as one of its poles, while the celestial equator is the intersection of the celestial sphere by the plane defined by the terrestrial equator. The observer’s meridian is the great semicircle PZSQ. For a star, X, then
 

(i) its azimuth is the arc NESA,
(ii) its altitude the arc AX,
(iii) its zenith distance the arc ZX;
(iv) its hour angle is ∠ZPX,
(v) its declination the arc BX
(vi) and its north polar distance the arc PX.