


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-11-2020
Date: 6-10-2020
Date: 26-1-2021
|

A semicubical parabola is a curve of the form
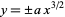 |
(1) |
(i.e., it is half a cubic, and hence has power  ). It has parametric equations
). It has parametric equations
 |
 |
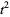 |
(2) |
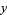 |
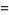 |
 |
(3) |
and the polar equation
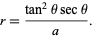 |
(4) |
The evolute of the parabola is a particular case of the semicubical parabola also called Neile's parabola or the cuspidal cubic. In Cartesian coordinates, it has equation
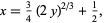 |
(5) |
which can also be written
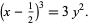 |
(6) |
The Tschirnhausen cubic catacaustic is also a semicubical parabola.
The semicubical parabola is the curve along which a particle descending under gravity describes equal vertical spacings within equal times, making it an isochronous curve. It was discovered by William Neile in 1657 and was the first nontrivial algebraic curve to have its arc length computed. Wallis published the method in 1659, giving Neile the credit (MacTutor Archive). The problem of finding the curve having this property had been posed by Leibniz in 1687 and was also solved by Huygens (MacTutor Archive).
The semicubical parabola is a singular member of the family Legendre normal form elliptic curves
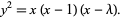 |
(7) |
The arc length, curvature, and tangential angle for  are
are
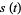 |
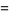 |
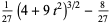 |
(8) |
 |
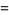 |
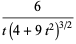 |
(9) |
 |
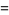 |
 |
(10) |
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 223-224, 1987.
Gray, A. "The Semicubical Parabola." §1.8 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 21-22, 1997.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 85-87, 1972.
MacTutor History of Mathematics Archive. "Neile's Semi-Cubical Parabola." https://www-groups.dcs.st-and.ac.uk/~history/Curves/Neiles.html.
Smith, D. E. History of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. New York: Dover, p. 330, 1958.
Yates, R. C. "Semi-Cubic Parabola." A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 186-187, 1952.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|