Znám's Problem

A problem posed by the Slovak mathematician Stefan Znám in 1972 asking whether, for all integers 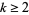, there exist  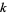integers  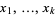all greater than 1 such that  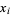is a proper divisor of  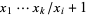for each 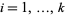. The answer is negative for  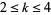(Jának and Skula 1978) and affirmative for  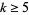(Sun Qi 1983). Sun Qi also gave a lower bound for the number  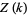of solutions.

All solutions for 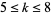 have now been computed, summarized in the table below. The numbers of solutions for 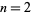, 3, ... terms are 0, 0, 0, 2, 5, 15, 93, ... (OEIS A075441), and the solutions themselves are given by OEIS A075461.

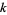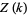		known solutions	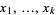references
2	0	--	Jának and Skula (1978)
3	0	--	Jának and Skula (1978)
4	0	--	Jának and Skula (1978)
5	2	2, 3, 7, 47, 395
		2, 3, 11, 23, 31
6	5	2, 3, 7, 43, 1823, 193667
		2, 3, 7, 47, 403, 19403
		2, 3, 7, 47, 415, 8111
		2, 3, 7, 47, 583, 1223
		2, 3, 7, 55, 179, 24323
7	15	2, 3, 7, 43, 1807, 3263447, 2130014000915	Jának and Skula (1978)
		2, 3, 7, 43, 1807, 3263591, 71480133827	Cao, Liu, and Zhang (1987)
		2, 3, 7, 43, 1807, 3264187, 14298637519
		2, 3, 7, 43, 3559, 3667, 33816127
		2, 3, 7, 47, 395, 779831, 6020372531
		2, 3, 7, 67, 187, 283, 334651
		2, 3, 11, 17, 101, 149, 3109
		2, 3, 11, 23, 31, 47063, 442938131
		2, 3, 11, 23, 31, 47095, 59897203
		2, 3, 11, 23, 31, 47131, 30382063
		2, 3, 11, 23, 31, 47243, 12017087
		2, 3, 11, 23, 31, 47423, 6114059
		2, 3, 11, 23, 31, 49759, 866923
		2, 3, 11, 23, 31, 60563, 211031
		2, 3, 11, 31, 35, 67, 369067
8	93		Brenton and Vasiliu (1998)
9	?	2, 3, 7, 43, 1807, 3263443,	Sun (1983)
		10650056950807,
		113423713055421844361000447,
		2572987736655734348107429290411162753668127385839515
10	?	2, 3, 11, 23, 31, 47059,	Sun (1983)
		2214502423, 4904020979258368507,
		24049421765006207593444550012151040547,
		115674937446230858658157460659985774139375256845351399814552547262816571295

Cao and Sun (1988) showed that 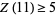 and Cao and Jing (1998) that there are  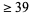solutions for 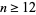. A solution for  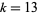was found by Girgensohn in 1996: 3, 4, 5, 7, 29, 41, 67, 89701, 230865947737, 5726348063558735709083, followed by large numbers having 45, 87, and 172 digits.

It has been observed that all known solutions to Znám's problem provide a decomposition of 1 as an Egyptian fraction

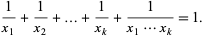Conversely, every solution to this Diophantine equation is a solution to Znám's problem, unless 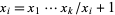 for some .

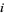REFERENCES:

Brenton, L. and Jaje, L. "Perfectly Weighted Graphs." Graphs Combin. 17, 389-407, 2001.

Brenton, L, and Vasiliu, A. "Znam's Problem." Math. Mag. 75, 3-11, 2002.

Cao, Z. and Jing, C. "On the Number of Solutions of Znám's Problem." J. Harbin Inst. Tech. 30, 46-49, 1998.

Cao, Z. and Sun, Q. "On the Equation 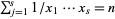 and the Number of Solutions of Znám's Problem." Northeast. Math. J. 4, 43-48, 1988.

Cao, Z.; Liu, R.; and Zhang, L. "On the Equation 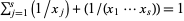 and Znám's Problem. J. Number Th. 27, 206-211, 1987.

Jának, J. and Skula, L. "On the Integers 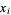 for which  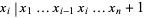Holds." Math. Slovaca 28, 305-310, 1978.

Sloane, N. J. A. Sequences A075441 and A075461 in "The On-Line Encyclopedia of Integer Sequences."

Sun, Q. "On a Problem of Š. Znám." Sichuan Daxue Xuebao, No. 4, 9-12, 1983.

Wayne State University Undergraduate Mathematics Research Group. "The Egyptian Fraction: The Unit Fraction Equation." https://www.math.wayne.edu/ugresearch/egyfra.html.