


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-2-2020
Date: 4-11-2020
Date: 7-6-2020
|
The Engel expansion, also called the Egyptian product, of a positive real number 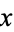 is the unique increasing sequence
is the unique increasing sequence 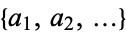 of positive integers
of positive integers 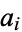 such that
such that
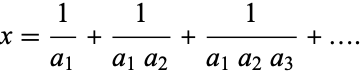 |
The following table gives the Engel expansions of Catalan's constant, e, the Euler-Mascheroni constant 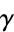 ,
, 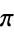 , and the golden ratio
, and the golden ratio 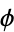 .
.
| constant | OEIS | Engel expansion |
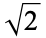 |
A028254 | 1, 3, 5, 5, 16, 18, 78, 102, 120, ... |
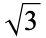 |
A028257 | 1, 2, 3, 3, 6, 17, 23, 25, 27, 73, ... |
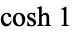 |
A118239 | 1, 2, 12, 30, 56, 90, 132, 182, ... |
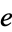 |
A000027 | 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... |
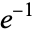 |
A059193 | 3, 10, 28, 54, 88, 130, 180, 238, 304, 378, ... |
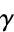 |
A053977 | 2, 7, 13, 19, 85, 2601, 9602, 46268, 4812284, ... |
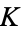 |
A054543 | 2, 2, 2, 4, 4, 5, 5, 12, 13, 41, 110, ... |
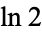 |
A059180 | 2, 3, 7, 9, 104, 510, 1413, 2386, ... |
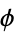 |
A028259 | 1, 2, 5, 6, 13, 16, 16, 38, 48, 58, 104, ... |
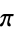 |
A006784 | 1, 1, 1, 8, 8, 17, 19, 300, 1991, 2492, ... |
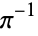 |
A014012 | 4, 4, 11, 45, 70, 1111, 4423, 5478, 49340, ... |
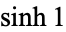 |
A068377 | 1, 6, 20, 42, 72, 110, 156, 210, ... |
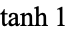 |
A118326 | 2, 2, 22, 50, 70, 29091, 49606, 174594, ... |
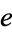 has a very regular Engel expansion, namely 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... (OEIS A000027). Interestingly, the expansion for the hyperbolic sine
has a very regular Engel expansion, namely 1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, ... (OEIS A000027). Interestingly, the expansion for the hyperbolic sine  has closed form
has closed form 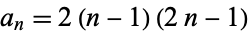 for
for 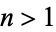 , which means the expansion for the hyperbolic cosine
, which means the expansion for the hyperbolic cosine 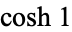 has the closed form
has the closed form 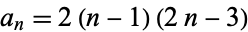 for
for 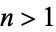 . Similarly, the Engel expansion for
. Similarly, the Engel expansion for 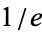 is
is 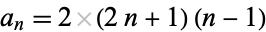 for
for 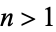 , which follows from
, which follows from
![e^(-1)=sum_(n=1)^infty[1/((2n)!)-1/((2n+1)!)].](https://mathworld.wolfram.com/images/equations/EngelExpansion/NumberedEquation2.gif) |
REFERENCES:
Engel, F. "Entwicklung der Zahlen nach Stammbruechen." Verhandlungen der 52. Versammlung deutscher Philologen und Schulmaenner in Marburg. pp. 190-191, 1913.
Erdős, P. and Shallit, J. O. "New Bounds on the Length of Finite Pierce and Engel Series." Sem. Theor. Nombres Bordeaux 3, 43-53, 1991.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 53-59, 2003.
Schweiger, F. Ergodic Theory of Fibred Systems and Metric Number Theory. Oxford, England: Oxford University Press, 1995.
Sloane, N. J. A. Sequences A000027/M0472, A006784/M4475, A014012, A028254, A028257, A028259, A053977, A054543, A059180, A059193, A068377, A118239, and A118326 in "The On-Line Encyclopedia of Integer Sequences."
Wu, J. "How Many Points Have the Same Engel and Sylvester Expansions?." J. Number Th. 103, 16-26, 2003.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|