


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-2-2021
Date: 1-1-2020
Date: 3-11-2020
|
Ramanujan calculated 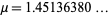 (Hardy 1999, Le Lionnais 1983, Berndt 1994), while the correct value is
(Hardy 1999, Le Lionnais 1983, Berndt 1994), while the correct value is
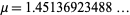 |
(OEIS A070769; Derbyshire 2004, p. 114). The first 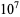 decimal digits were computed by E. Weisstein on Oct. 7, 2013.
decimal digits were computed by E. Weisstein on Oct. 7, 2013.
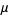 -constant primes occur for 4, 144, 227, 444, 19474, ... (OEIS A122422) decimal digits.
-constant primes occur for 4, 144, 227, 444, 19474, ... (OEIS A122422) decimal digits.
The Earls sequence (starting position of 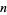 copies of the digit
copies of the digit 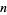 ) for
) for 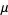 is given for
is given for 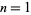 , 2, ... by 3, 42, 178, 10013, 31567, 600035, 1253449, ... (OEIS A229071).
, 2, ... by 3, 42, 178, 10013, 31567, 600035, 1253449, ... (OEIS A229071).
The starting positions of the first occurrence of 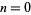 , 1, 2, ... in the decimal expansion of
, 1, 2, ... in the decimal expansion of 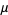 (not including the initial 0 to the left of the decimal point) are 17, 1, 8, 5, 2, 3, 6, 34, 11, ... (OEIS A229201).
(not including the initial 0 to the left of the decimal point) are 17, 1, 8, 5, 2, 3, 6, 34, 11, ... (OEIS A229201).
Scanning the decimal expansion of 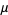 until all
until all 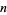 -digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 7, 465, 102, 5858, 48441, ... (OEIS A000000), which end at digits 34, 512, 7454, 92508, 1414058, ... (OEIS A000000).
-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 7, 465, 102, 5858, 48441, ... (OEIS A000000), which end at digits 34, 512, 7454, 92508, 1414058, ... (OEIS A000000).
The digit sequences 0123456789 and 9876543210 do not occur in the first 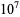 digits (E. Weisstein, Oct. 7, 2013).
digits (E. Weisstein, Oct. 7, 2013).
It is not known if 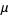 is normal, but the following table giving the counts of digits in the first
is normal, but the following table giving the counts of digits in the first 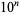 terms shows that the decimal digits are very uniformly distributed up to at least
terms shows that the decimal digits are very uniformly distributed up to at least 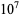 .
.
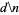 |
OEIS | 10 | 100 | 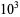 |
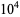 |
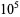 |
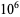 |
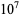 |
| 0 | A000000 | 0 | 9 | 116 | 1053 | 10098 | 100104 | 999785 |
| 1 | A000000 | 1 | 7 | 100 | 970 | 9893 | 100238 | 1000370 |
| 2 | A000000 | 1 | 9 | 106 | 979 | 10113 | 100057 | 999594 |
| 3 | A000000 | 2 | 13 | 109 | 1012 | 10120 | 99999 | 1001006 |
| 4 | A000000 | 2 | 10 | 96 | 1019 | 10118 | 99822 | 999546 |
| 5 | A000000 | 1 | 15 | 103 | 994 | 9912 | 99918 | 1001007 |
| 6 | A000000 | 1 | 8 | 89 | 1036 | 10060 | 99971 | 999430 |
| 7 | A000000 | 0 | 6 | 97 | 988 | 10029 | 100141 | 997185 |
| 8 | A000000 | 1 | 15 | 101 | 988 | 9838 | 100089 | 1001593 |
| 9 | A000000 | 1 | 8 | 83 | 961 | 9819 | 99661 | 1000484 |
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 123-124, 1994.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 23 and 45, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 39, 1983.
Sloane, N. J. A. Sequences A070769, A122422, A229071, A229201 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|