Paris Constant

The golden ratio 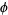 can be written in terms of a nested radical in the beautiful form

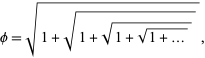(1)

which can be written recursively as

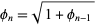(2)

for 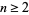, with .

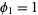Paris (1987) proved 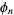 approaches  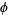at a constant rate, namely

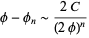(3)

as 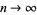, where

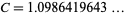(4)

(OEIS A105415) is the Paris constant.

A product formula for 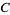 is given by

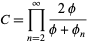(5)

(Finch 2003, p. 8).

Another formula is given by letting 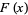 be the analytic solution to the functional equation

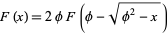(6)

for 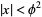, subject to initial conditions  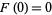and 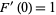. Then

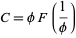(7)

(Finch 2003, p. 8).

A close approximation is 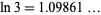, which is good to 4 decimal places (M. Stark, pers. comm.).

REFERENCES:

Finch, S. R. "Analysis of a Radical Expansion." §1.2.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, p. 8, 2003.

Paris, R. B. "An Asymptotic Approximation Connected with the Golden Number." Amer. Math. Monthly 94, 272-278, 1987.

Plouffe, S. "The Paris Constant." https://pi.lacim.uqam.ca/piDATA/paris.txt.

Sloane, N. J. A. Sequence A105415 in "The On-Line Encyclopedia of Integer Sequences."