BBP Formula

The BBP (named after Bailey-Borwein-Plouffe) is a formula for calculating pi discovered by Simon Plouffe in 1995,

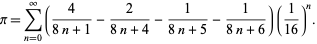Amazingly, this formula is a digit-extraction algorithm for 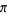 in base 16.

Following the discovery of this and related formulas, similar formulas in other bases were investigated. This class of formulas are now known as BBP-type formulas.

REFERENCES:

Adamchik, V. and Wagon, S. "A Simple Formula for 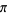." Amer. Math. Monthly 104, 852-855, 1997.

Adamchik, V. and Wagon, S. "Pi: A 2000-Year Search Changes Direction." http://www-2.cs.cmu.edu/~adamchik/articles/pi.htm.

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 31, 2007.

Bailey, D. H. "A Compendium of BBP-Type Formulas for Mathematical Constants." 28 Nov 2000. http://crd.lbl.gov/~dhbailey/dhbpapers/bbp-formulas.pdf.

Bailey, D. H. "nth digit of pi" math-fun@cs.arizona.edu mailing list. 31 Oct 2002.

Bailey, D. H.; Borwein, P. B.; and Plouffe, S. "On the Rapid Computation of Various Polylogarithmic Constants." Math. Comput. 66, 903-913, 1997.

Bailey, D. H.; Borwein, J. M.; Kapoor, V.; and Weisstein, E. W. "Ten Problems in Experimental Mathematics." Amer. Math. Monthly 113, 481-509, 2006.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.

Finch, S. R. "Archimedes' Constant." §1.4 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 17-28, 2003.

Gourdon, X. and Sebah, P. "Collection of Series for 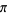." http://numbers.computation.free.fr/Constants/Pi/piSeries.html.

Plouffe, S. "The Story Behind a Formula for Pi." sci.math and sci.math.symbolic newsgroup posting. 23 Jun 2003.