Erdős-Borwein Constant

The Erdős-Borwein constant 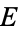, sometimes also denoted 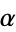, is the sum of the reciprocals of the Mersenne numbers,

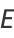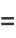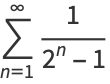			(1)
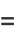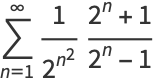			(2)
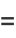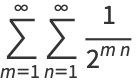			(3)
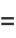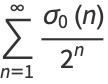			(4)
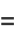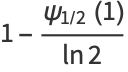			(5)
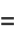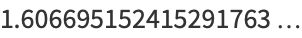			(6)

(OEIS A065442), where 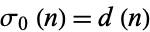 is the number of divisors of  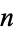and 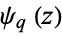 is a q-polygamma function. The transformation from equation (1) to (2) follows from the series transformation

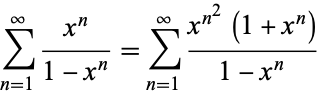(7)

due to Clausen in 1828 (Knuth 1998, pp. 155 and 157), with .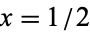

Erdős (1948) showed that the constant 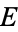 is irrational. Borwein (1992) subsequently showed that

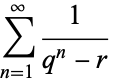(8)

with 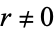 is irrational.

REFERENCES:

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Borwein, P. "On the Irrationality of Certain Series." Math. Proc. Cambridge Philos. Soc. 112, 141-146, 1992.

Erdős, P. "On Arithmetical Properties of Lambert Series." J. Indian Math. Soc. 12, 63-66, 1948.

Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 354-361, 2003.

Knuth, D. E. The Art of Computer Programming, Vol. 3: Sorting and Searching, 2nd ed. Reading, MA: Addison-Wesley, 1998.

Sloane, N. J. A. Sequence A065442 in "The On-Line Encyclopedia of Integer Sequences."