


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-11-2020
Date: 1-9-2020
Date: 14-10-2020
|
Let 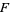 be the set of complex analytic functions
be the set of complex analytic functions 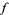 defined on an open region containing the set closure of the unit disk
defined on an open region containing the set closure of the unit disk 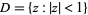 satisfying
satisfying 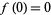 and
and 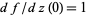 . For each
. For each 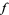 in
in 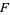 , let
, let 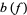 be the supremum of all numbers
be the supremum of all numbers 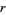 such that there is a subregion
such that there is a subregion 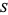 in
in 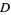 on which
on which  is one-to-one and such that
is one-to-one and such that 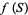 contains a disk of radius
contains a disk of radius 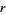 . In 1925, Bloch (Conway 1989) showed that
. In 1925, Bloch (Conway 1989) showed that 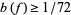 .
.
Define Bloch's constant by
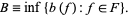 |
(1) |
Ahlfors and Grunsky (1937) derived
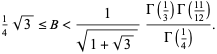 |
(2) |
Bonk (1990) proved that 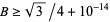 , which was subsequently improved to
, which was subsequently improved to 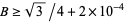 (Chen and Gauthier 1996; Xiong 1998; Finch 2003, p. 456).
(Chen and Gauthier 1996; Xiong 1998; Finch 2003, p. 456).
Ahlfors and Grunsky (1937) also conjectured that the upper limit is actually the value of 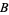 ,
,
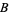 |
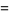 |
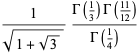 |
(3) |
 |
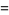 |
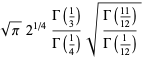 |
(4) |
 |
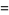 |
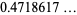 |
(5) |
(OEIS A085508; Le Lionnais 1983).
REFERENCES:
Ahlfors, L. V. and Grunsky, H. "Über die Blochsche Konstante." Math. Zeit. 42, 671-673, 1937.
Bonk, M. "On Bloch's Constant." Proc. Amer. Math. Soc. 110, 889-894, 1990.
Chen, H. and Gauthier, P. M. "On Bloch's Constant." J. d'Analyse Math. 69, 275-291, 1996.
Conway, J. B. Functions of One Complex Variable I, 2nd ed. New York: Springer-Verlag, 1989.
Finch, S. R. "Bloch-Landau Constants." §7.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 456-459, 2003.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 25, 1983.
Minda, C. D. "Bloch Constants." J. d'Analyse Math. 41, 54-84, 1982.
Sloane, N. J. A. Sequence A085508 in "The On-Line Encyclopedia of Integer Sequences."
Xiong, C. "Lower Bound of Bloch's Constant." Nanjing Daxue Xuebao Shuxue Bannian Kan 15, 174-179, 1998.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|