


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-1-2021
Date: 28-10-2020
Date: 6-1-2020
|
Ball tetrahedron picking is the selection of quadruples of points (corresponding to vertices of a general tetrahedron) randomly placed inside a ball. 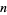 random tetrahedra can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[],
random tetrahedra can be picked in a unit ball in the Wolfram Language using the function RandomPoint[Ball[], 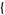 n, 4
n, 4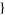 ].
].
The mean tetrahedron volume of a tetrahedron formed by four random points in a unit ball is
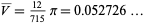 |
(OEIS A093591; Hostinsky 1925; Solomon 1978, p. 124; Zinani 2003).
REFERENCES:
Groemer, H. "On Some Mean Values Associated with a Randomly Selected Simplex in a Convex Set." Pacific J. Math. 45, 525-533, 1973.
Hostinsky, B. "Sur les probabilités géométriques." Publ. Fac. Sci. Univ. Masaryk, No. 50. Brno, Czechoslovakia, 1925.
Kingman, J. F. C. "Random Secants of a Convex Body." J. Appl. Prob. 6, 660-672, 1969.
Sloane, N. J. A. Sequence A093591 in "The On-Line Encyclopedia of Integer Sequences."
Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, 1978.
Zinani, A. "The Expected Volume of a Tetrahedron Whose Vertices are Chosen at Random in the Interior of a Cube." Monatshefte Math. 139, 341-348, 2003.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|