Egyptian Fraction

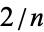An Egyptian fraction is a sum of positive (usually) distinct unit fractions. The famous Rhind papyrus, dated to around 1650 BC contains a table of representations of  as Egyptian fractions for odd  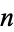between 5 and 101. The reason the Egyptians chose this method for representing fractions is not clear, although André Weil characterized the decision as "a wrong turn" (Hoffman 1998, pp. 153-154). The unique fraction that the Egyptians did not represent using unit fractions was 2/3 (Wells 1986, p. 29).

Egyptian fractions are almost always required to exclude repeated terms, since representations such as 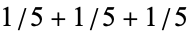 are trivial. Any rational number has representations as an Egyptian fraction with arbitrarily many terms and with arbitrarily large denominators, although for a given fixed number of terms, there are only finitely many. Fibonacci proved that any fraction can be represented as a sum of distinct unit fractions (Hoffman 1998, p. 154). An infinite chain of unit fractions can be constructed using the identity

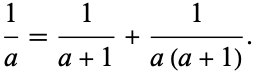(1)

Martin (1999) showed that for every positive rational number, there exist Egyptian fractions whose largest denominator is at most 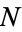 and whose denominators form a positive proportion of the integers up to  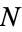for sufficiently large 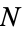. Each fraction  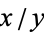with 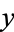 odd has an Egyptian fraction in which each denominator is odd (Breusch 1954; Guy 1994, p. 160). Every  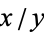has a 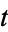-term representation where  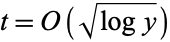(Vose 1985).

No algorithm is known for producing unit fraction representations having either a minimum number of terms or smallest possible denominator (Hoffman 1998, p. 155). However, there are a number of algorithms (including the binary remainder method, continued fraction unit fraction algorithm, generalized remainder method, greedy algorithm, reverse greedy algorithm, small multiple method, and splitting algorithm) for decomposing an arbitrary fraction into unit fractions. In 1202, Fibonacci published an algorithm for constructing unit fraction representations, and this algorithm was subsequently rediscovered by Sylvester (Hoffman 1998, p. 154; Martin 1999).

Taking the fractions 1/2, 1/3, 2/3, 1/4, 2/4, 3/4, ... (the numerators of which are OEIS A002260, and the denominators of which are 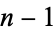 copies of the integer 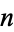), the unit fraction representations using the greedy algorithm are

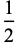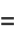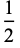			(2)
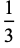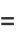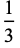			(3)
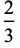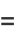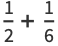			(4)
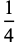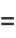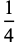			(5)
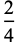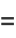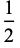			(6)
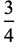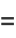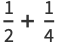			(7)
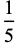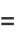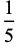			(8)
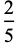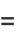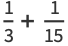			(9)
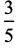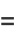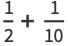			(10)
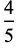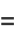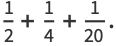			(11)

The number of terms in these representations are 1, 1, 2, 1, 1, 2, 1, 2, 2, 3, 1, ... (OEIS A050205). The minimum denominators for each representation are given by 2, 3, 2, 4, 2, 2, 5, 3, 2, 2, 6, 3, 2, ... (OEIS A050206), and the maximum denominators are 2, 3, 6, 4, 2, 4, 5, 15, 10, 20, 6, 3, 2, ... (OEIS A050210).

The Egyptian fractions for various constants using the greedy algorithm are summarized in the following table.

constant	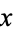OEIS	Egyptian fraction for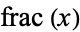
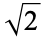	A006487	3, 13, 253, 218201, 61323543802, ...
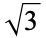	A118325	2, 5, 32, 1249, 5986000, 438522193400489, ...
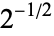	A069139	2, 5, 141, 68575, 32089377154, ...
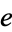	A006525	2, 5, 55, 9999, 3620211523, 25838201785967533906, ...
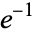	A006526	3, 29, 15786, 513429610, 339840390654894740, ...
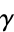	A110820	2, 13, 3418, 52016149, 153922786652714666, ...
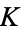	A118323	2, 3, 13, 176, 36543, ...
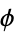	A117116	2, 9, 145, 37986, 2345721887, ...
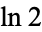	A118324	2, 6, 38, 6071, 144715221, ...
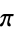	A001466	8, 61, 5020, 128541455, 162924332716605980, ...
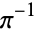	A006524	4, 15, 609, 845029, 1010073215739, ...

Any fraction with odd denominator can be represented as a finite sum of unit fractions, each having an odd denominator (Starke 1952, Breusch 1954). Graham proved that infinitely many fractions with a certain range can be represented as a sum of units fractions with square denominators (Hoffman 1998, p. 156).

Paul Erdős and E. G. Straus have conjectured that the Diophantine equation

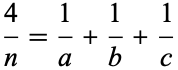(12)

always can be solved, an assertion sometimes known as the Erdős-Straus conjecture, and Sierpiński (1956) conjectured that

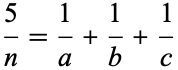(13)

can be solved (Guy 1994).

The harmonic number 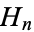 is never an integer except for 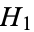. This result was proved in 1915 by Taeisinger, and the more general results that any number of consecutive terms not necessarily starting with 1 never sum to an integer was proved by Kürschák in 1918 (Hoffman 1998, p. 157). In 1932, Erdős proved that the sum of the reciprocals of any number of equally spaced integers is never a reciprocal.

Nontrivial sets of integers are known whose reciprocals sum to small integers. For example, there exists a set of 366 positive integers (with maximum 992) whose sum of reciprocals is exactly 2 (Mackenzie 1997; Martin). A similar set of 453 small positive integers is known that sums to 6 (Martin).

REFERENCES:

Beck, A.; Bleicher, M. N.; and Crowe, D. W. Excursions into Mathematics. New York: Worth Publishers, 1970.

Beeckmans, L. "The Splitting Algorithm for Egyptian Fractions." J. Number Th. 43, 173-185, 1993.

Bleicher, M. N. "A New Algorithm for the Expansion of Continued Fractions." J. Number Th. 4, 342-382, 1972.

Breusch, R. "A Special Case of Egyptian Fractions." Solution to advanced problem 4512. Amer. Math. Monthly 61, 200-201, 1954.

Eppstein, D. "Ten Algorithms for Egyptian Fractions." Mathematica Educ. Res. 4, 5-15, 1995.

Eppstein, D. "Egyptian Fractions." http://www.ics.uci.edu/~eppstein/numth/egypt/.

Eppstein, D. Egypt.ma Mathematica notebook. http://www.ics.uci.edu/~eppstein/numth/egypt/egypt.ma.

Gardner, M. "Mathematical Games: In Which a Mathematical Aesthetic is Applied to Modern Minimal Art." Sci. Amer. 239, 22-32, Nov. 1978.

Gardner, M. "Babylonian and Egyptian Mathematics, an Egyptian Historical Gap, Installments 1-3." http://www.teleport.com/~ddonahue/phresour.html

Golomb, S. W. "An Algebraic Algorithm for the Representation Problems of the Ahmes Papyrus." Amer. Math. Monthly 69, 785-786, 1962.

Graham, R. "On Finite Sums of Unit Fractions." Proc. London Math. Soc. 14, 193-207, 1964.

Guy, R. K. "Egyptian Fractions." §D11 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 158-166, 1994.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 153-157, 1998.

Ke, Z. and Sun, Q. "On the Representation of 1 by Unit Fractions." Sichuan Daxue Xuebao 1, 13-29, 1964.

Keith, M. "Egyptian Unit Fractions." http://mathpages.com/home/kmath340.htm.

Klee, V. and Wagon, S. Old and New Unsolved Problems in Plane Geometry and Number Theory. Washington, DC: Math. Assoc. Amer., pp. 175-177 and 206-208, 1991.

Loy, J. "Egyptian Fractions." http://www.jimloy.com/egypt/fraction.htm.

Martin, G. "Dense Egyptian Fractions." Trans. Amer. Math. Soc. 351, 3641-3657, 1999.

Martin, G. Egyptian fraction summing to 2. http://www.math.ubc.ca/~gerg/papers/downloads/recsum2.pdf.

Martin, G. Egyptian fraction summing to 6. http://www.math.ubc.ca/~gerg/papers/downloads/recsum6.pdf.

Mackenzie, D. "Fractions to Make an Egyptian Scribe Blanch." Science 278, 224, 1997.

MathPages. "Egyptian Unit Fractions." http://www.mathpages.com/home/kmath340.htm.

Niven, I. and Zuckerman, H. S. An Introduction to the Theory of Numbers, 5th ed. New York: Wiley, p. 200, 1991.

Séroul, R. "Egyptian Fractions." §8.8 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 181-187, 2000.

Sierpiński, W. "Sur les décompositiones de nombres rationelles en fractions primaires." Mathesis 65, 16-32, 1956.

Sloane, N. J. A. Sequences A001466/M4553, A002260, A006487/M2962, A006524/M3509, A006525/M1553, A006526/M3122, A050205, A050206, A050210, A069139, A110820, A118323, A118324, and A118325 in "The On-Line Encyclopedia of Integer Sequences."

Starke, E. P. "Problem 4512." Amer. Math. Monthly 59, 640, 1952.

Stewart, I. "The Riddle of the Vanishing Camel." Sci. Amer. 266, 122-124, June 1992.

Tenenbaum, G. and Yokota, H. "Length and Denominators of Egyptian Fractions." J. Number Th. 35, 150-156, 1990.

Vose, M. "Egyptian Fractions." Bull. London Math. Soc. 17, 21, 1985.

Wagon, S. "Egyptian Fractions." §8.6 in Mathematica in Action. New York: W. H. Freeman, pp. 271-277, 1991.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 29, 1986.