


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-4-2020
Date: 12-12-2020
Date: 12-10-2020
|
The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron. It is denoted 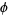 , or sometimes
, or sometimes  .
.
The designations "phi" (for the golden ratio conjugate 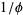 ) and "Phi" (for the larger quantity
) and "Phi" (for the larger quantity 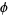 ) are sometimes also used (Knott), although this usage is not necessarily recommended.
) are sometimes also used (Knott), although this usage is not necessarily recommended.
The term "golden section" (in German, goldener Schnitt or der goldene Schnitt) seems to first have been used by Martin Ohm in the 1835 2nd edition of his textbook Die Reine Elementar-Mathematik (Livio 2002, p. 6). The first known use of this term in English is in James Sulley's 1875 article on aesthetics in the 9th edition of the Encyclopedia Britannica. The symbol 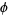 ("phi") was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490-430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5-6). Similarly, the alternate notation
("phi") was apparently first used by Mark Barr at the beginning of the 20th century in commemoration of the Greek sculptor Phidias (ca. 490-430 BC), who a number of art historians claim made extensive use of the golden ratio in his works (Livio 2002, pp. 5-6). Similarly, the alternate notation  is an abbreviation of the Greek tome, meaning "to cut."
is an abbreviation of the Greek tome, meaning "to cut."
In the Season 1 episode "Sabotage" (2005) of the television crime drama NUMB3RS, math genius Charlie Eppes mentions that the golden ratio is found in the pyramids of Giza and the Parthenon at Athens. Similarly, the character Robert Langdon in the novel The Da Vinci Code makes similar such statements (Brown 2003, pp. 93-95). However, claims of the significance of the golden ratio appearing prominently in art, architecture, sculpture, anatomy, etc., tend to be greatly exaggerated.
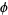 has surprising connections with continued fractions and the Euclidean algorithm for computing the greatest common divisor of two integers.
has surprising connections with continued fractions and the Euclidean algorithm for computing the greatest common divisor of two integers.
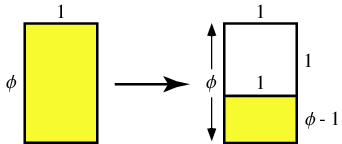
Given a rectangle having sides in the ratio 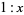 ,
, 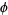 is defined as the unique number
is defined as the unique number  such that partitioning the original rectangle into a square and new rectangle as illustrated above results in a new rectangle which also has sides in the ratio
such that partitioning the original rectangle into a square and new rectangle as illustrated above results in a new rectangle which also has sides in the ratio 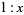 (i.e., such that the yellow rectangles shown above are similar). Such a rectangle is called a golden rectangle, and successive points dividing a golden rectangle into squares lie on a logarithmic spiral, giving a figure known as a whirling square.
(i.e., such that the yellow rectangles shown above are similar). Such a rectangle is called a golden rectangle, and successive points dividing a golden rectangle into squares lie on a logarithmic spiral, giving a figure known as a whirling square.
Based on the above definition, it can immediately be seen that
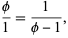 |
(1) |
giving
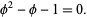 |
(2) |
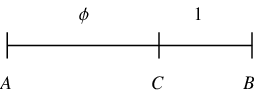
Euclid ca. 300 BC gave an equivalent definition of 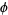 by defining it in terms of the so-called "extreme and mean ratios" on a line segment, i.e., such that
by defining it in terms of the so-called "extreme and mean ratios" on a line segment, i.e., such that
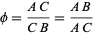 |
(3) |
for the line segment 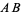 illustrated above (Livio 2002, pp. 3-4). Plugging in,
illustrated above (Livio 2002, pp. 3-4). Plugging in,
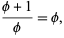 |
(4) |
and clearing denominators gives
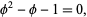 |
(5) |
which is exactly the same formula obtained above (and incidentally means that 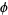 is an algebraic number of degree 2.) Using the quadratic equation and taking the positive sign (since the figure is defined so that
is an algebraic number of degree 2.) Using the quadratic equation and taking the positive sign (since the figure is defined so that 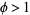 ) gives the exact value of
) gives the exact value of 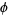 , namely
, namely
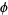 |
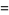 |
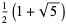 |
(6) |
 |
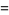 |
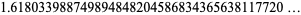 |
(7) |
(OEIS A001622). Prime numbers appearing in consecutive digits of the decimal expansion (starting with the first) are known as phi-primes.
In an apparent blatant misunderstanding of the difference between an exact quantity and an approximation, the character Robert Langdon in the novel The Da Vinci Code incorrectly defines the golden ratio to be exactly 1.618 (Brown 2003, pp. 93-95).
The legs of a golden triangle (an isosceles triangle with a vertex angle of 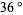 ) are in a golden ratio to its base and, in fact, this was the method used by Pythagoras to construct
) are in a golden ratio to its base and, in fact, this was the method used by Pythagoras to construct 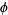 . The ratio of the circumradius to the length of the side of a decagon is also
. The ratio of the circumradius to the length of the side of a decagon is also 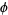 ,
,
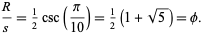 |
(8) |
Bisecting a (schematic) Gaullist cross also gives a golden ratio (Gardner 1961, p. 102).
Exact trigonometric formulas for 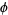 include
include
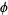 |
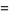 |
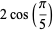 |
(9) |
 |
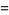 |
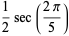 |
(10) |
 |
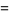 |
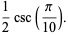 |
(11) |
The golden ratio is given by the series
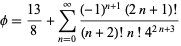 |
(12) |
(B. Roselle). Another fascinating connection with the Fibonacci numbers is given by the series
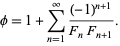 |
(13) |
A representation in terms of a nested radical is
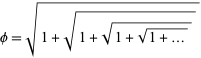 |
(14) |
(Livio 2002, p. 83). This is equivalent to the recurrence equation
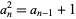 |
(15) |
with 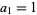 , giving
, giving 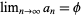 .
.
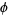 is the "worst" real number for rational approximation because its continued fraction representation
is the "worst" real number for rational approximation because its continued fraction representation
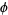 |
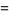 |
![[1,1,1,...]](http://mathworld.wolfram.com/images/equations/GoldenRatio/Inline41.gif) |
(16) |
 |
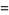 |
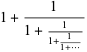 |
(17) |
(OEIS A000012; Williams 1979, p. 52; Steinhaus 1999, p. 45; Livio 2002, p. 84) has the smallest possible term (1) in each of its infinitely many denominators, thus giving convergents that converge more slowly than any other continued fraction. In particular, the convergents 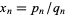 are given by the quadratic recurrence equation
are given by the quadratic recurrence equation
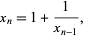 |
(18) |
with 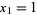 , which has solution
, which has solution
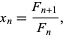 |
(19) |
where 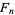 is the
is the 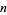 th Fibonacci number. This gives the first few convergents as 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, ... (OEIS A000045 and A000045), which are good to 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, ... (OEIS A114540) decimal digits, respectively.
th Fibonacci number. This gives the first few convergents as 1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, ... (OEIS A000045 and A000045), which are good to 0, 0, 0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 5, ... (OEIS A114540) decimal digits, respectively.
As a result,
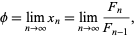 |
(20) |
as first proved by Scottish mathematician Robert Simson in 1753 (Wells 1986, p. 62; Livio 2002, p. 101).
The golden ratio also satisfies the recurrence relation
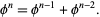 |
(21) |
Taking 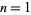 gives the special case
gives the special case
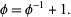 |
(22) |
Treating (21) as a linear recurrence equation
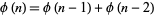 |
(23) |
in 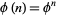 , setting
, setting 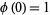 and
and 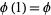 , and solving gives
, and solving gives
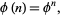 |
(24) |
as expected. The powers of the golden ratio also satisfy
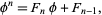 |
(25) |
where 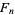 is a Fibonacci number (Wells 1986, p. 39).
is a Fibonacci number (Wells 1986, p. 39).
The sine of certain complex numbers involving 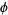 gives particularly simple answers, for example
gives particularly simple answers, for example
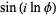 |
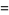 |
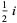 |
(26) |
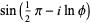 |
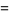 |
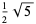 |
(27) |
(D. Hoey, pers. comm.).
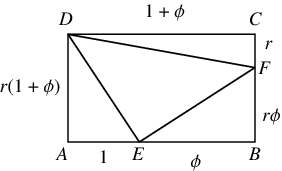
In the figure above, three triangles can be inscribed in the rectangle 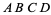 of arbitrary aspect ratio
of arbitrary aspect ratio 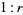 such that the three right triangles have equal areas by dividing
such that the three right triangles have equal areas by dividing 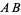 and
and 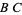 in the golden ratio. Then
in the golden ratio. Then
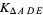 |
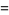 |
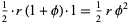 |
(28) |
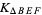 |
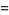 |
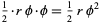 |
(29) |
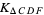 |
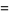 |
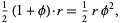 |
(30) |
which are all equal. The converse is also true, namely if the adjacent sides of a rectangle are divided in any ratio and connected in the same way, then if the areas of the three outer triangles are all equal, both divided sides are in the golden ratio (D. J. Lewis, pers. comm., Jun. 11, 2009).

The substitution system
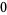 |
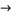 |
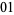 |
(31) |
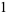 |
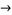 |
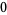 |
(32) |
gives
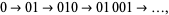 |
(33) |
giving rise to the sequence
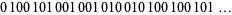 |
(34) |
(OEIS A003849). Here, the zeros occur at positions 1, 3, 4, 6, 8, 9, 11, 12, ... (OEIS A000201), and the ones occur at positions 2, 5, 7, 10, 13, 15, 18, ... (OEIS A001950). These are complementary Beatty sequences generated by 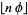 and
and 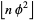 . This sequence also has many connections with the Fibonacci numbers. It is plotted above (mod 2) as a recurrence plot.
. This sequence also has many connections with the Fibonacci numbers. It is plotted above (mod 2) as a recurrence plot.
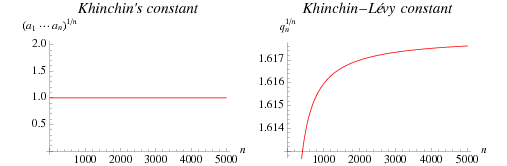
Let the continued fraction of 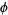 be denoted
be denoted ![[a_0;a_1,a_2,...]](http://mathworld.wolfram.com/images/equations/GoldenRatio/Inline83.gif) and let the denominators of the convergents be denoted
and let the denominators of the convergents be denoted 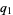 ,
, 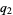 , ...,
, ...,  . As can be seen from the plots above, the regularity in the continued fraction of
. As can be seen from the plots above, the regularity in the continued fraction of 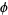 means that
means that 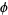 is one of a set of numbers of measure 0 whose continued fraction sequences do not converge to Khinchin's constant or the Lévy constant.
is one of a set of numbers of measure 0 whose continued fraction sequences do not converge to Khinchin's constant or the Lévy constant.
The golden ratio has Engel expansion 1, 2, 5, 6, 13, 16, 16, 38, 48, 58, 104, ... (OEIS A028259).
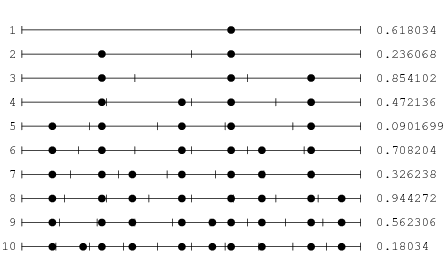
Steinhaus (1999, pp. 48-49) considers the distribution of the fractional parts of 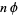 in the intervals bounded by 0,
in the intervals bounded by 0, 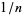 ,
, 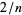 , ...,
, ..., 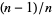 , 1, and notes that they are much more uniformly distributed than would be expected due to chance (i.e.,
, 1, and notes that they are much more uniformly distributed than would be expected due to chance (i.e., 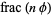 is close to an equidistributed sequence). In particular, the number of empty intervals for
is close to an equidistributed sequence). In particular, the number of empty intervals for 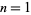 , 2, ..., are a mere 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, ... (OEIS A036414). The values of
, 2, ..., are a mere 0, 0, 0, 0, 0, 0, 1, 0, 2, 0, 1, 1, 0, 2, 2, ... (OEIS A036414). The values of 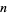 for which no bins are left blank are then given by 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, ... (OEIS A036415). Steinhaus (1983) remarks that the highly uniform distribution has its roots in the continued fraction for
for which no bins are left blank are then given by 1, 2, 3, 4, 5, 6, 8, 10, 13, 16, 21, 34, 55, 89, 144, ... (OEIS A036415). Steinhaus (1983) remarks that the highly uniform distribution has its roots in the continued fraction for 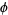 .
.
The sequence 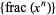 , of power fractional parts, where
, of power fractional parts, where 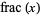 is the fractional part, is equidistributed for almost all real numbers
is the fractional part, is equidistributed for almost all real numbers 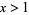 , with the golden ratio being one exception.
, with the golden ratio being one exception.
Salem showed that the set of Pisot numbers is closed, with 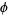 the smallest accumulation point of the set (Le Lionnais 1983).
the smallest accumulation point of the set (Le Lionnais 1983).
REFERENCES:
Bogomolny, A. "Golden Ratio in Geometry." http://www.cut-the-knot.org/do_you_know/GoldenRatio.shtml.
Boyer, C. B. History of Mathematics. New York: Wiley, p. 56, 1968.
Brown, D. The Da Vinci Code. New York: Doubleday, 2003.
Coxeter, H. S. M. "The Golden Section, Phyllotaxis, and Wythoff's Game." Scripta Mathematica 19, 135-143, 1953.
Dixon, R. Mathographics. New York: Dover, pp. 30-31 and 50, 1991.
Finch, S. R. "The Golden Mean." §1.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 5-12, 2003.
Gardner, M. "Phi: The Golden Ratio." Ch. 8 in The Second Scientific American Book of Mathematical Puzzles & Diversions, A New Selection. New York: Simon and Schuster, pp. 89-103, 1961.
Gardner, M. "Notes on a Fringe-Watcher: The Cult of the Golden Ratio." Skeptical Inquirer 18, 243-247, 1994.
Hambridge, J. The Elements of Dynamic Stability. New York: Dover, 1967.
Herz-Fischler, R. A Mathematical History of the Golden Number. New York: Dover, 1998.
Hofstetter, K. "A Simple Construction of the Golden Ratio." Forum Geom. 2, 65-66, 2002. http://forumgeom.fau.edu/FG2002volume2/FG200208index.html.
Hofstetter, K. "A 4-Step Construction of the Golden Ratio." Forum Geom. 6, 179-180, 2006. http://forumgeom.fau.edu/FG2006volume6/FG200618index.html.
Huntley, H. E. The Divine Proportion. New York: Dover, 1970.
Knott, R. "Fibonacci Numbers and the Golden Section." http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 40, 1983.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, 2002.
Markowsky, G. "Misconceptions About the Golden Ratio." College Math. J. 23, 2-19, 1992.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 122-134, 1990.
Ohm, M. die Reine Elementar-Mathematik. Berlin: Jonas Veilags-Buchhandlung, 1835.
Olariu, A. "Golden Section and the Art of Painting." 18 Aug 1999. http://arxiv.org/abs/physics/9908036.
Pappas, T. "Anatomy & the Golden Section." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 32-33, 1989.
Saaty, T. L. and Kainen, P. C. The Four-Color Problem: Assaults and Conquest. New York: Dover, p. 148, 1986.
Sloane, N. J. A. Sequences A000012/M0003, A000201/M2322, A001622/M4046, A001950/M1332, A003849, A028259, A036414, A036415, and A114540 in "The On-Line Encyclopedia of Integer Sequences."
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, p. 45, 1999.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 175, 2004. http://www.mathematicaguidebooks.org/.
van Zanten, A. J. "The Golden Ratio in the Arts of Painting, Building, and Mathematics." Nieuw Arch. Wisk. 17, 229-245, 1999.
Walser, R. Der Goldene Schnitt. Stuttgart, Germany: Teubner, 1993.
Weisstein, E. W. "Books about Golden Ratio." http://www.ericweisstein.com/encyclopedias/books/GoldenRatio.html.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 36-49, 1986.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 87-88, 1991.
Williams, R. "The Golden Proportion." §2-7 in The Geometrical Foundation of Natural Structure: A Source Book of Design. New York: Dover, pp. 52-53, 1979.
Zeising, A. Neue Lehre von den Proportionen des menschlichen Körpers, aus einem bisher unerkannt gebliebenen, die ganze Natur und Kunst durchdringenden morphologischen Grundgesetze entwickelt und mit einer vollständigen historischen Uebersicht der bisherigen Systeme begleitet. Leipzig, Germany: Weigel, 1854.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|