Almost Integer

An almost integer is a number that is very close to an integer.

Surprising examples are given by

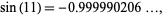(1)

which equals 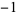 to within 5 digits and

(2)

which equals 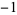 to within 16 digits (M. Trott, pers. comm., Dec. 7, 2004). The first of these comes from the half-angle formula identity

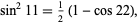(3)

where 22 is the numerator of the convergent 22/7 t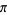o , so 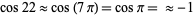. It therefore follows that any pi approximation  gives a near-identity of the form .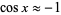

Another surprising example involving both e and pi is

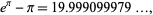(4)

which can also be written as

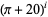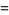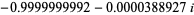			(5)
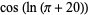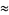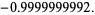			(6)

Here, 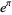 is Gelfond's constant. Applying cosine a few more times gives

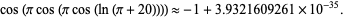(7)

This curious near-identity was apparently noticed almost simultaneously around 1988 by N. J. A. Sloane, J. H. Conway, and S. Plouffe, but no satisfying explanation as to "why"  is true has yet been discovered.

Another nested cosine almost integer is given by

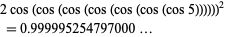(8)

(P. Rolli, pers. comm., Feb. 19, 2004).

An example attributed to Ramanujan is

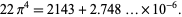(9)

Some near-identities involving integers and the logarithm are

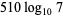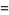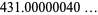			(10)
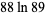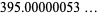			(11)
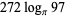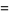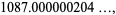			(12)

which are good to 6, 6, and 6 decimal digits, respectively (K. Hammond, pers. comm., Jan. 4 and Mar. 23-24, 2006).

An interesting near-identity is given by

(13)

(W. Dubuque, pers. comm.).

Near-identities involving 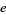 and 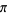 are given by

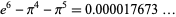(14)

(D. Wilson, pers. comm.),

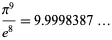(15)

(D. Ehlke, pers. comm., Apr. 7, 2005),

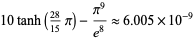(16)

(Povolotsky, pers. comm., May 11, 2008), and

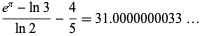(17)

(good to 8 digits; M. Stay, pers. comm., Mar. 17, 2009), or equivalently

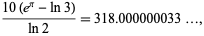(18)

Other remarkable near-identities are given by

(19)

where 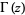 is the gamma function (S. Plouffe, pers. comm.),

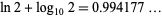(20)

(D. Davis, pers. comm.),

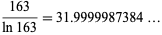(21)

(posted to sci.math; origin unknown),

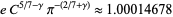(22)

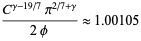(23)

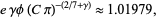(24)

where 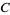 is Catalan's constant,  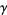is the Euler-Mascheroni constant, and  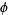is the golden ratio (D. Barron, pers. comm.), and

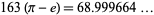(25)

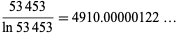(26)

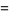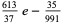			(27)
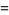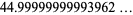			(28)

(E. Stoschek, pers. comm.). Stoschek also gives an interesting near-identity involving the fine structure constant 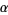 and Feigenbaum constant ,

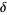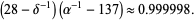(29)

E. Pegg Jr. (pers. comm., Mar. 4, 2002) discovered the interesting near-identities

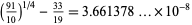(30)

and

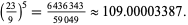(31)

The near-identity

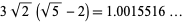(32)

arises by noting that the augmentation ratio 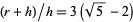 in the augmentation of the dodecahedron to form the great dodecahedron is approximately equal to 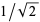. Another near identity is given by

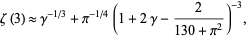(33)

where 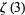 is Apéry's constant and  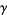is the Euler-Mascheroni constant, which is accurate to four digits (P. Galliani, pers. comm., April 19, 2002).

J. DePompeo (pers. comm., Mar. 29, 2004) found

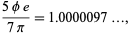(34)

which is equal to 1 to five digits.

M. Hudson (pers. comm., Oct. 18, 2004) noted the almost integer

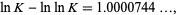(35)

where 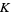 is Khinchin's constant, as well as

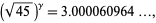(36)

(pers. comm., Feb. 4, 2005), where 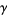 is the Euler-Mascheroni constant.

M. Joseph found

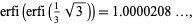(37)

which is equal to 1 to four digits (pers. comm., May 18, 2006). M. Kobayashi (pers. comm., Sept. 17, 2004) found

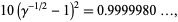(38)

which is equal to 1 to five digits. The related expression

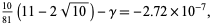(39)

which is equal to 0 to six digits (E. Pegg Jr., pers. comm., Sept. 28, 2004). S. M. Edde (pers. comm., Sep. 7, 2007) noted that

(40)

where 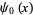 is the digamma function.

E. W. Weisstein (Mar. 17, 2003) found the almost integers

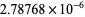			(41)
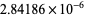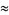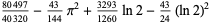			(42)
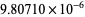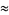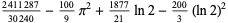			(43)

as individual integrals in the decomposition of the integration region to compute the average area of a triangle in triangle triangle picking.

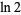 and 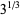 give the almost integer

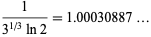(44)

(E. W. Weisstein, Feb. 5, 2005).

Prudnikov et al. (1986, p. 757) inadvertently give an almost integer result by incorrectly identifying the infinite product

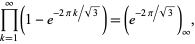(45)

where 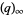 is a q-Pochhammer symbol, as being equal 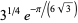, which differs from the correct result by

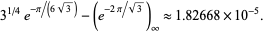(46)

A much more obscure almost identity related to the eight curve is the location of the jump in

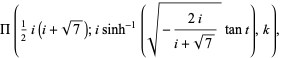(47)

where

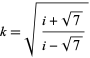(48)

and 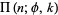 is an elliptic integral of the third kind, which is 1.3333292798..., or within  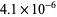of 4/3 (E. W. Weisstein, Apr. 2006). Another slightly obscure one is the value of  needed to give a 99.5% confidence interval for a Student's t-distribution with sample size 30, which is 2.7499956..., or within 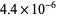 of 11/4 (E. W. Weisstein, May 2, 2006).

Let 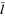 be the average length of a line in triangle line picking for an isosceles right triangle, then

(49)

which is within 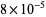 of .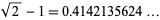

D. Terr (pers. comm., July 29, 2004) found the almost integer

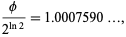(50)

where 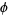 is the golden ratio and  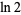is the natural logarithm of 2.

A set of almost integers due to D. Hickerson are those of the form

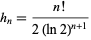(51)

for 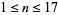, as summarized in the following table.

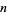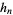0	0.72135
1	1.04068
2	3.00278
3	12.99629
4	74.99874
5	541.00152
6	4683.00125
7	47292.99873
8	545834.99791
9	7087261.00162
10	102247563.00527
11	1622632572.99755
12	28091567594.98157
13	526858348381.00125
14	10641342970443.08453
15	230283190977853.03744
16	5315654681981354.51308
17	130370767029135900.45799

These numbers are close to integers due to the fact that the quotient is the dominant term in an infinite series for the number of possible outcomes of a race between 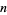 people (where ties are allowed). Calling this number 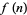, it follows that

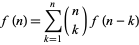(52)

with 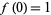, where  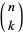is a binomial coefficient. From this, we obtain the exponential generating function for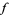 

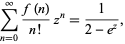(53)

and then by contour integration it can be shown that

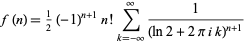(54)

for 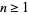, where  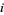is the square root of  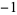and the sum is over all integers  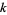(here, the imaginary parts of the terms for  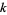and 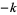 cancel each other, so this sum is real). The  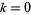term dominates, so  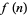is asymptotic to 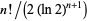. The sum can be done explicitly as

(55)

where 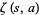 is the Hurwitz zeta function. In fact, the other terms are quite small for  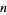from 1 to 15, so  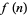is the nearest integer to  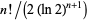for these values, given by the sequence 1, 3, 13 75, 541, 4683, ... (OEIS A034172).

A large class of irrational "almost integers" can be found using the theory of modular functions, and a few rather spectacular examples are given by Ramanujan (1913-14). Such approximations were also studied by Hermite (1859), Kronecker (1863), and Smith (1965). They can be generated using some amazing (and very deep) properties of the j-function. Some of the numbers which are closest approximations to integers are 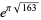 (sometimes known as the Ramanujan constant and which corresponds to the field  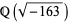which has class number 1 and is the imaginary quadratic field of maximal discriminant), 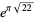, , 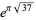and 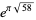, the last three of which have class number 2 and are due to Ramanujan (Berndt 1994, Waldschmidt 1988ab).

The properties of the j-function also give rise to the spectacular identity

(56)

(Le Lionnais 1983, p. 152; Trott 2004, p. 8).

The list below gives numbers of the form 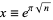 for 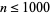 for which .

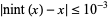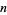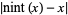25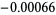
37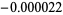
43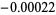
58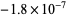
67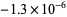
74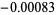
148	0.00097
163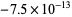
232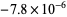
268	0.00029
522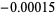
652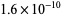
719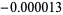

Gosper (pers. comm.) noted that the expression

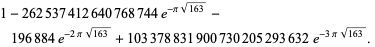(57)

differs from an integer by a mere .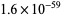

E. Pegg Jr. noted that the triangle dissection illustrated above has length

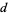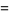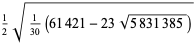			(58)
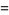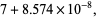			(59)

which is almost an integer.

Borwein and Borwein (1992) and Borwein et al. (2004, pp. 11-15) give examples of series identities that are nearly true. For example,

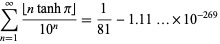(60)

which is true since 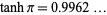 and 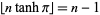 for positive integer . In fact, the first few doubled values of 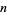 at which  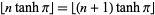are 268, 536, 804, 1072, 1341, 1609, ...(OEIS A096613).

An example of a (very) near-integer is

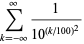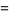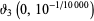			(61)
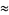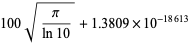			(62)

(Borwein and Borwein 1992; Maze and Minder 2005).

Maze and Minder (2005) found the class of near-identities obtained from

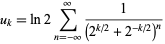(63)

as

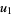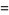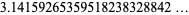			(64)
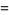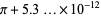			(65)
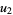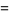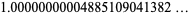			(66)
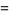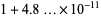			(67)
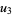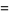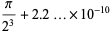			(68)
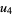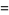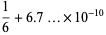			(69)
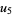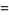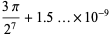			(70)
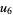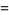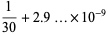			(71)

(OEIS A114609 and A114610). Here, the excesses can be computed as exact sums connected by a recurrence relation, with the first few being

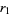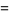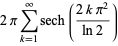			(72)
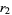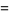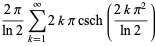			(73)

(Maze and Minder 2005). These sums can also be done in closed form using q-polygamma functions 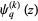, giving for example

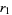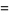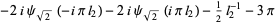			(74)
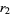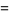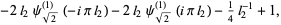			(75)

with .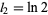

An amusing almost integer involving units of length is given by

(76)

If combinations of physical and mathematical constants are allowed and taken in SI units, the following quantities have a near-integer numeric prefactor

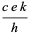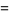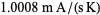			(77)
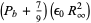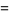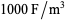			(78)

(M. Trott, pers. comm. Apr. 28, 2011), the first of which was apparently noticed by Weisskopf. Here, 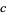 is the speed of light,  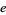is the elementary charge,  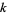is Boltzmann's constant,  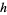is Planck's constant,  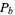is the bond percolation threshold for a 4-dimensional hypercube lattice,  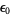is the vacuum permittivity, and  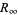is the Rydberg constant. Another famous example of this sort is Wyler's constant, which approximates the (dimensionless) fine structure constant in terms of fundamental mathematical constants.

REFERENCES:

Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 90-91, 1994.

Borwein, J.; Bailey, D.; and Girgensohn, R. "High Precision Fraud." §1.4 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, pp. 11-15, 2004.

Borwein, J. M. and Borwein, P. B. "Strange Series and High Precision Fraud." Amer. Math. Monthly 99, 622-640, 1992.

Cohen, H. "Elliptic Curves." In From Number Theory to Physics (Ed. M. Waldschmidt, P. Moussa, J.-M. Luck, and C. Itzykson). New York: Springer-Verlag, pp. 212-237, 1992.

Hermite, C. "Sur la théorie des équations modulaires." Comptes Rendus Acad. Sci. Paris 48, 1079-1084 and 1095-1102, 1859.

Hermite, C. "Sur la théorie des équations modulaires." Comptes Rendus Acad. Sci. Paris 49, 16-24, 110-118, and 141-144, 1859.

Kronecker, L. "Über die Klassenzahl der aus Wurzeln der Einheit gebildeten komplexen Zahlen." Monatsber. K. Preuss. Akad. Wiss. Berlin, 340-345. 1863.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, 1983.

Maze, G. and Minder, L. "A New Family of Almost Identities." 28 Jun 2005. https://www.arxiv.org/abs/math.GM/0409014/.

Pegg, E. Jr. https://www.mathpuzzle.com/WIWWTP.gif.

Pegg, E. Jr. "Math Games: Keen Approximations." Feb. 14, 2005. https://www.maa.org/editorial/mathgames/mathgames_02_14_05.html.

Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions. New York: Gordon & Breach, 1986.

Ramanujan, S. "Modular Equations and Approximations to 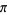." Quart. J. Pure Appl. Math. 45, 350-372, 1913-14.

Roberts, J. The Lure of the Integers. Washington, DC: Math. Assoc. Amer., 1992.

Sloane, N. J. A. Sequences A034172, A096613, A114609, and A114610 in "The On-Line Encyclopedia of Integer Sequences."

Smith, H. J. S. Report on the Theory of Numbers. New York: Chelsea, 1965.

Stillwell, J. "Modular Miracles." Amer. Math. Monthly 108, 70-76, 2001.

Stoschek, E. "Modul 33: Algames with Numbers." https://marvin.sn.schule.de/~inftreff/modul33/task33.htm.

Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. https://www.mathematicaguidebooks.org/.

Waldschmidt, M. "Some Transcendental Aspects of Ramanujan's Work." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, pp. 57-76, 1988a.

Waldschmidt, M. In Ramanujan Centennial International Conference (Ed. R. Balakrishnan, K. S. Padmanabhan, and V. Thangaraj). Ramanujan Math. Soc., 1988b.