Class Number

For any ideal 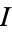 in a Dedekind ring, there is an ideal  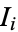such that

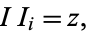(1)

where 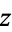 is a principal ideal, (i.e., an ideal of rank 1). Moreover, for a Dedekind ring with a finite ideal class group, there is a finite list of ideals  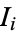such that this equation may be satisfied for some 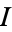. The size of this list is known as the class number.

Class numbers are usually studied in the context of the orders of number fields. If this order is maximal, then it is the ring of integers of the number field, in which case the class number is equal to the order of the class group of the number field; otherwise it is equal to the order of the Picard group of the nonmaximal order in question.

When the class number of a ring of integers in a number field is 1, the ring corresponding to a given ideal has unique factorization and, in a sense, the class number is a measure of the failure of unique factorization in that ring.

A finite series giving exactly the class number of a ring is known as a class number formula. A class number formula is known for the full ring of cyclotomic integers, as well as for any subring of the cyclotomic integers. Finding the class number is a computationally difficult problem.

The Wolfram Language function NumberFieldClassNumber[Sqrt[d]] gives the class numbe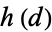r  for 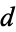 a fundamental discriminant.

The class number 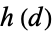 of an order of a quadratic field with discriminant  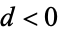is equal to the number of reduced binary quadratic forms of discriminant 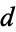. For example, the class number  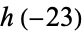of the ring of integers  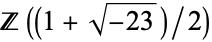of the number field  is equal to 3 since there are three reduced binary quadratic forms of discriminant 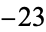, namely 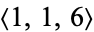, , 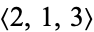and 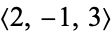. An inefficient way to compute the class number  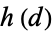of the unique order of the quadratic number field  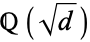with discriminant  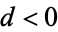is to count the number of reduced binary quadratic forms with discriminant .

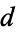Some fairly sophisticated mathematics shows that the class number for discriminant 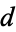 can be given by the class number formula

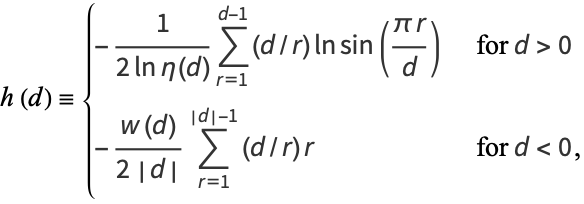(2)

where 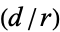 is the Kronecker symbol,  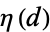is the fundamental unit,  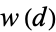is the number of substitutions which leave the binary quadratic form unchanged

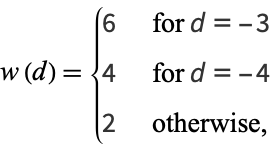(3)

and the sums are taken over all terms where the Kronecker symbol is defined (Cohn 1980). The class number for 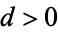 can also be written

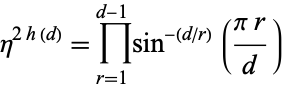(4)

for 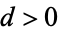, where the product is taken over terms for which the Kronecker symbol is defined.

The class number 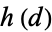 is related to the Dirichlet L-series by

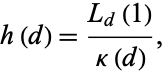(5)

where 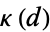 is the Dirichlet structure constant.

Oesterlé (1985) showed that class number 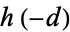 satisfies the inequality

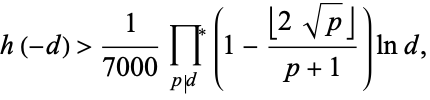(6)

for 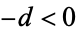, where  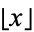is the floor function, the product is over primes dividing 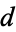, and the  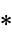indicates that the greatest prime factor of  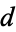is omitted from the product. It is also known that if  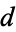is relatively prime to 5077, then the denominator 7000 in (6) can be replaced by 55.

Gauss's class number problem asks to determine a complete list of fundamental binary quadratic form discriminants 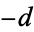 such that the class number is given by  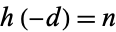for a given 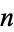. This problem has been solved for  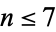and odd 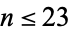. Gauss conjectured that the class number  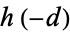of an imaginary quadratic field with binary quadratic form discriminant  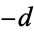tends to infinity with 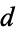, an assertion now known as Gauss's class number conjecture.

The negated discriminants 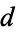 corresponding to imaginary quadratic fields are 3, 4, 7, 8, 11, 15, 19, 20, 23, 24, 31, 35, 39, 40, 43, ... (OEIS A003657), which have corresponding class numbers 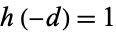, 1, 1, 1, 1, 2, 1, 2, 3, 2, 3, 2, 4, 2, 1, ... (OEIS A006641).

The complete set of negative discriminants having class numbers 1-5 and odd 7-23 are known. Buell (1977) gives the smallest and largest class numbers for fundamental discriminants with 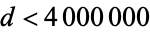, partitioned into even discriminants, discriminants 1 (mod 8), and discriminants 5 (mod 8). Arno et al. (1993) give complete lists of values of fundamental  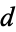with 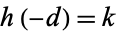 for odd 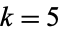, 7, 9, ..., 23. Wagner (1996) gives complete lists of values for 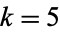, 6, and 7. Lists of negative fundamental discriminants corresponding to imaginary quadratic fields  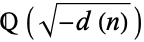having small class numbers  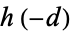are given in the table below. In the table,  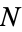is the number of fundamental values of  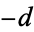with a given class number 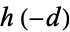, where "fundamental" means that  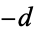is not divisible by any square number  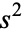such that 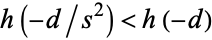. For example, although 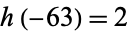,  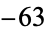is not a fundamental discriminant since  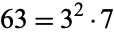and 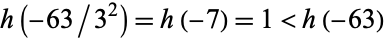. Even values  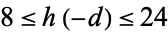have been computed by Weisstein.

The following table lists the fundamental discriminants 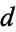 having class numbers  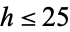(Cohen 1993, pp. 229 and 514-515; Cox 1997, p. 271). The search was terminated at 50000, 70000, 90000, and 90000 for class numbers 18, 20, 22, and 24, respectively. As far as I know, analytic upper bounds are not currently known for these cases.

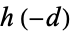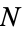		Sloane
1	9	A014602	3, 4, 7, 8, 11, 19, 43, 67, 163
2	18	A014603	15, 20, 24, 35, 40, 51, 52, 88, 91, 115, 123, 148, 187, 232, 235, 267, 403, 427
3	16	A006203	23, 31, 59, 83, 107, 139, 211, 283, 307, 331, 379, 499, 547, 643, 883, 907
4	54	A013658	39, 55, 56, 68, 84, 120, 132, 136, 155, 168, 184, 195, 203, 219, 228, 259, 280, 291, 292, 312, 323, 328, 340, 355, 372, 388, 408, 435, 483, 520, 532, 555, 568, 595, 627, 667, 708, 715, 723, 760, 763, 772, 795, 955, 1003, 1012, 1027, 1227, 1243, 1387, 1411, 1435, 1507, 1555
5	25	A046002	47, 79, 103, 127, 131, 179, 227, 347, 443, 523, 571, 619, 683, 691, 739, 787, 947, 1051, 1123, 1723, 1747, 1867, 2203, 2347, 2683
6	51	A046003	87, 104, 116, 152, 212, 244, 247, 339, 411, 424, 436, 451, 472, 515, 628, 707, 771, 808, 835, 843, 856, 1048, 1059, 1099, 1108, 1147, 1192, 1203, 1219, 1267, 1315, 1347, 1363, 1432, 1563, 1588, 1603, 1843, 1915, 1963, 2227, 2283, 2443, 2515, 2563, 2787, 2923, 3235, 3427, 3523, 3763
7	31	A046004	71, 151, 223, 251, 463, 467, 487, 587, 811, 827, 859, 1163, 1171, 1483, 1523, 1627, 1787, 1987, 2011, 2083, 2179, 2251, 2467, 2707, 3019, 3067, 3187, 3907, 4603, 5107, 5923
8	131	A046005	95, 111, 164, 183, 248, 260, 264, 276, 295, 299, 308, 371, 376, 395, 420, 452, 456, 548, 552, 564, 579, 580, 583, 616, 632, 651, 660, 712, 820, 840, 852, 868, 904, 915, 939, 952, 979, 987, 995, 1032, 1043, 1060, 1092, 1128, 1131, 1155, 1195, 1204, 1240, 1252, 1288, 1299, 1320, 1339, 1348, 1380, 1428, 1443, 1528, 1540, 1635, 1651, 1659, 1672, 1731, 1752, 1768, 1771, 1780, 1795, 1803, 1828, 1848, 1864, 1912, 1939, 1947, 1992, 1995, 2020, 2035, 2059, 2067, 2139, 2163, 2212, 2248, 2307, 2308, 2323, 2392, 2395, 2419, 2451, 2587, 2611, 2632, 2667, 2715, 2755, 2788, 2827, 2947, 2968, 2995, 3003, 3172, 3243, 3315, 3355, 3403, 3448, 3507, 3595, 3787, 3883, 3963, 4123, 4195, 4267, 4323, 4387, 4747, 4843, 4867, 5083, 5467, 5587, 5707, 5947, 6307
9	34	A046006	199, 367, 419, 491, 563, 823, 1087, 1187, 1291, 1423, 1579, 2003, 2803, 3163, 3259, 3307, 3547, 3643, 4027, 4243, 4363, 4483, 4723, 4987, 5443, 6043, 6427, 6763, 6883, 7723, 8563, 8803, 9067, 10627
10	87	A046007	119, 143, 159, 296, 303, 319, 344, 415, 488, 611, 635, 664, 699, 724, 779, 788, 803, 851, 872, 916, 923, 1115, 1268, 1384, 1492, 1576, 1643, 1684, 1688, 1707, 1779, 1819, 1835, 1891, 1923, 2152, 2164, 2363, 2452, 2643, 2776, 2836, 2899, 3028, 3091, 3139, 3147, 3291, 3412, 3508, 3635, 3667, 3683, 3811, 3859, 3928, 4083, 4227, 4372, 4435, 4579, 4627, 4852, 4915, 5131, 5163, 5272, 5515, 5611, 5667, 5803, 6115, 6259, 6403, 6667, 7123, 7363, 7387, 7435, 7483, 7627, 8227, 8947, 9307, 10147, 10483, 13843
11	41	A046008	167, 271, 659, 967, 1283, 1303, 1307, 1459, 1531, 1699, 2027, 2267, 2539, 2731, 2851, 2971, 3203, 3347, 3499, 3739, 3931, 4051, 5179, 5683, 6163, 6547, 7027, 7507, 7603, 7867, 8443, 9283, 9403, 9643, 9787, 10987, 13003, 13267, 14107, 14683, 15667
12	206	A046009	231, 255, 327, 356, 440, 516, 543, 655, 680, 687, 696, 728, 731, 744, 755, 804, 888, 932, 948, 964, 984, 996, 1011, 1067, 1096, 1144, 1208, 1235, 1236, 1255, 1272, 1336, 1355, 1371, 1419, 1464, 1480, 1491, 1515, 1547, 1572, 1668, 1720, 1732, 1763, 1807, 1812, 1892, 1955, 1972, 2068, 2091, 2104, 2132, 2148, 2155, 2235, 2260, 2355, 2387, 2388, 2424, 2440, 2468, 2472, 2488, 2491, 2555, 2595, 2627, 2635, 2676, 2680, 2692, 2723, 2728, 2740, 2795, 2867, 2872, 2920, 2955, 3012, 3027, 3043, 3048, 3115, 3208, 3252, 3256, 3268, 3304, 3387, 3451, 3459, 3592, 3619, 3652, 3723, 3747, 3768, 3796, 3835, 3880, 3892, 3955, 3972, 4035, 4120, 4132, 4147, 4152, 4155, 4168, 4291, 4360, 4411, 4467, 4531, 4552, 4555, 4587, 4648, 4699, 4708, 4755, 4771, 4792, 4795, 4827, 4888, 4907, 4947, 4963, 5032, 5035, 5128, 5140, 5155, 5188, 5259, 5299, 5307, 5371, 5395, 5523, 5595, 5755, 5763, 5811, 5835, 6187, 6232, 6235, 6267, 6283, 6472, 6483, 6603, 6643, 6715, 6787, 6843, 6931, 6955, 6963, 6987, 7107, 7291, 7492, 7555, 7683, 7891, 7912, 8068, 8131, 8155, 8248, 8323, 8347, 8395, 8787, 8827, 9003, 9139, 9355, 9523, 9667, 9843, 10003, 10603, 10707, 10747, 10795, 10915, 11155, 11347, 11707, 11803, 12307, 12643, 14443, 15163, 15283, 16003, 17803
13	37	A046010	191, 263, 607, 631, 727, 1019, 1451, 1499, 1667, 1907, 2131, 2143, 2371, 2659, 2963, 3083, 3691, 4003, 4507, 4643, 5347, 5419, 5779, 6619, 7243, 7963, 9547, 9739, 11467, 11587, 11827, 11923, 12043, 14347, 15787, 16963, 20563
14	95	A046011	215, 287, 391, 404, 447, 511, 535, 536, 596, 692, 703, 807, 899, 1112, 1211, 1396, 1403, 1527, 1816, 1851, 1883, 2008, 2123, 2147, 2171, 2335, 2427, 2507, 2536, 2571, 2612, 2779, 2931, 2932, 3112, 3227, 3352, 3579, 3707, 3715, 3867, 3988, 4187, 4315, 4443, 4468, 4659, 4803, 4948, 5027, 5091, 5251, 5267, 5608, 5723, 5812, 5971, 6388, 6499, 6523, 6568, 6979, 7067, 7099, 7147, 7915, 8035, 8187, 8611, 8899, 9115, 9172, 9235, 9427, 10123, 10315, 10363, 10411, 11227, 12147, 12667, 12787, 13027, 13435, 13483, 13603, 14203, 16867, 18187, 18547, 18643, 20227, 21547, 23083, 30067
15	68	A046012	239, 439, 751, 971, 1259, 1327, 1427, 1567, 1619, 2243, 2647, 2699, 2843, 3331, 3571, 3803, 4099, 4219, 5003, 5227, 5323, 5563, 5827, 5987, 6067, 6091, 6211, 6571, 7219, 7459, 7547, 8467, 8707, 8779, 9043, 9907, 10243, 10267, 10459, 10651, 10723, 11083, 11971, 12163, 12763, 13147, 13963, 14323, 14827, 14851, 15187, 15643, 15907, 16603, 16843, 17467, 17923, 18043, 18523, 19387, 19867, 20707, 22003, 26203, 27883, 29947, 32323, 34483
16	322	A046013	399, 407, 471, 559, 584, 644, 663, 740, 799, 884, 895, 903, 943, 1015, 1016, 1023, 1028, 1047, 1139, 1140, 1159, 1220, 1379, 1412, 1416, 1508, 1560, 1595, 1608, 1624, 1636, 1640, 1716, 1860, 1876, 1924, 1983, 2004, 2019, 2040, 2056, 2072, 2095, 2195, 2211, 2244, 2280, 2292, 2296, 2328, 2356, 2379, 2436, 2568, 2580, 2584, 2739, 2760, 2811, 2868, 2884, 2980, 3063, 3108, 3140, 3144, 3160, 3171, 3192, 3220, 3336, 3363, 3379, 3432, 3435, 3443, 3460, 3480, 3531, 3556, 3588, 3603, 3640, 3732, 3752, 3784, 3795, 3819, 3828, 3832, 3939, 3976, 4008, 4020, 4043, 4171, 4179, 4180, 4216, 4228, 4251, 4260, 4324, 4379, 4420, 4427, 4440, 4452, 4488, 4515, 4516, 4596, 4612, 4683, 4687, 4712, 4740, 4804, 4899, 4939, 4971, 4984, 5115, 5160, 5187, 5195, 5208, 5363, 5380, 5403, 5412, 5428, 5460, 5572, 5668, 5752, 5848, 5860, 5883, 5896, 5907, 5908, 5992, 5995, 6040, 6052, 6099, 6123, 6148, 6195, 6312, 6315, 6328, 6355, 6395, 6420, 6532, 6580, 6595, 6612, 6628, 6708, 6747, 6771, 6792, 6820, 6868, 6923, 6952, 7003, 7035, 7051, 7195, 7288, 7315, 7347, 7368, 7395, 7480, 7491, 7540, 7579, 7588, 7672, 7707, 7747, 7755, 7780, 7795, 7819, 7828, 7843, 7923, 7995, 8008, 8043, 8052, 8083, 8283, 8299, 8308, 8452, 8515, 8547, 8548, 8635, 8643, 8680, 8683, 8715, 8835, 8859, 8932, 8968, 9208, 9219, 9412, 9483, 9507, 9508, 9595, 9640, 9763, 9835, 9867, 9955, 10132, 10168, 10195, 10203, 10227, 10312, 10387, 10420, 10563, 10587, 10635, 10803, 10843, 10948, 10963, 11067, 11092, 11107, 11179, 11203, 11512, 11523, 11563, 11572, 11635, 11715, 11848, 11995, 12027, 12259, 12387, 12523, 12595, 12747, 12772, 12835, 12859, 12868, 13123, 13192, 13195, 13288, 13323, 13363, 13507, 13795, 13819, 13827, 14008, 14155, 14371, 14403, 14547, 14707, 14763, 14995, 15067, 15387, 15403, 15547, 15715, 16027, 16195, 16347, 16531, 16555, 16723, 17227, 17323, 17347, 17427, 17515, 18403, 18715, 18883, 18907, 19147, 19195, 19947, 19987, 20155, 20395, 21403, 21715, 21835, 22243, 22843, 23395, 23587, 24403, 25027, 25267, 27307, 27787, 28963, 31243
17	45	A046014	383, 991, 1091, 1571, 1663, 1783, 2531, 3323, 3947, 4339, 4447, 4547, 4651, 5483, 6203, 6379, 6451, 6827, 6907, 7883, 8539, 8731, 9883, 11251, 11443, 12907, 13627, 14083, 14779, 14947, 16699, 17827, 18307, 19963, 21067, 23563, 24907, 25243, 26083, 26107, 27763, 31627, 33427, 36523, 37123
18	150	A046015	335, 519, 527, 679, 1135, 1172, 1207, 1383, 1448, 1687, 1691, 1927, 2047, 2051, 2167, 2228, 2291, 2315, 2344, 2644, 2747, 2859, 3035, 3107, 3543, 3544, 3651, 3688, 4072, 4299, 4307, 4568, 4819, 4883, 5224, 5315, 5464, 5492, 5539, 5899, 6196, 6227, 6331, 6387, 6484, 6739, 6835, 7323, 7339, 7528, 7571, 7715, 7732, 7771, 7827, 8152, 8203, 8212, 8331, 8403, 8488, 8507, 8587, 8884, 9123, 9211, 9563, 9627, 9683, 9748, 9832, 10228, 10264, 10347, 10523, 11188, 11419, 11608, 11643, 11683, 11851, 11992, 12067, 12148, 12187, 12235, 12283, 12651, 12723, 12811, 12952, 13227, 13315, 13387, 13747, 13947, 13987, 14163, 14227, 14515, 14667, 14932, 15115, 15243, 16123, 16171, 16387, 16627, 17035, 17131, 17403, 17635, 18283, 18712, 19027, 19123, 19651, 20035, 20827, 21043, 21652, 21667, 21907, 22267, 22443, 22507, 22947, 23347, 23467, 23683, 23923, 24067, 24523, 24667, 24787, 25435, 26587, 26707, 28147, 29467, 32827, 33763, 34027, 34507, 36667, 39307, 40987, 41827, 43387, 48427
19	47	A046016	311, 359, 919, 1063, 1543, 1831, 2099, 2339, 2459, 3343, 3463, 3467, 3607, 4019, 4139, 4327, 5059, 5147, 5527, 5659, 6803, 8419, 8923, 8971, 9619, 10891, 11299, 15091, 15331, 16363, 16747, 17011, 17299, 17539, 17683, 19507, 21187, 21211, 21283, 23203, 24763, 26227, 27043, 29803, 31123, 37507, 38707
20	350	A046017	455, 615, 776, 824, 836, 920, 1064, 1124, 1160, 1263, 1284, 1460, 1495, 1524, 1544, 1592, 1604, 1652, 1695, 1739, 1748, 1796, 1880, 1887, 1896, 1928, 1940, 1956, 2136, 2247, 2360, 2404, 2407, 2483, 2487, 2532, 2552, 2596, 2603, 2712, 2724, 2743, 2948, 2983, 2987, 3007, 3016, 3076, 3099, 3103, 3124, 3131, 3155, 3219, 3288, 3320, 3367, 3395, 3496, 3512, 3515, 3567, 3655, 3668, 3684, 3748, 3755, 3908, 3979, 4011, 4015, 4024, 4036, 4148, 4264, 4355, 4371, 4395, 4403, 4408, 4539, 4548, 4660, 4728, 4731, 4756, 4763, 4855, 4891, 5019, 5028, 5044, 5080, 5092, 5268, 5331, 5332, 5352, 5368, 5512, 5560, 5592, 5731, 5944, 5955, 5956, 5988, 6051, 6088, 6136, 6139, 6168, 6280, 6339, 6467, 6504, 6648, 6712, 6755, 6808, 6856, 7012, 7032, 7044, 7060, 7096, 7131, 7144, 7163, 7171, 7192, 7240, 7428, 7432, 7467, 7572, 7611, 7624, 7635, 7651, 7667, 7720, 7851, 7876, 7924, 7939, 8067, 8251, 8292, 8296, 8355, 8404, 8472, 8491, 8632, 8692, 8755, 8808, 8920, 8995, 9051, 9124, 9147, 9160, 9195, 9331, 9339, 9363, 9443, 9571, 9592, 9688, 9691, 9732, 9755, 9795, 9892, 9976, 9979, 10027, 10083, 10155, 10171, 10291, 10299, 10308, 10507, 10515, 10552, 10564, 10819, 10888, 11272, 11320, 11355, 11379, 11395, 11427, 11428, 11539, 11659, 11755, 11860, 11883, 11947, 11955, 12019, 12139, 12280, 12315, 12328, 12331, 12355, 12363, 12467, 12468, 12472, 12499, 12532, 12587, 12603, 12712, 12883, 12931, 12955, 12963, 13155, 13243, 13528, 13555, 13588, 13651, 13803, 13960, 14307, 14331, 14467, 14491, 14659, 14755, 14788, 15235, 15268, 15355, 15603, 15688, 15691, 15763, 15883, 15892, 15955, 16147, 16228, 16395, 16408, 16435, 16483, 16507, 16612, 16648, 16683, 16707, 16915, 16923, 17067, 17187, 17368, 17563, 17643, 17763, 17907, 18067, 18163, 18195, 18232, 18355, 18363, 19083, 19443, 19492, 19555, 19923, 20083, 20203, 20587, 20683, 20755, 20883, 21091, 21235, 21268, 21307, 21387, 21508, 21595, 21723, 21763, 21883, 22387, 22467, 22555, 22603, 22723, 23443, 23947, 24283, 24355, 24747, 24963, 25123, 25363, 26635, 26755, 26827, 26923, 27003, 27955, 27987, 28483, 28555, 29107, 29203, 30283, 30787, 31003, 31483, 31747, 31987, 32923, 33163, 34435, 35683, 35995, 36283, 37627, 37843, 37867, 38347, 39187, 39403, 40243, 40363, 40555, 40723, 43747, 47083, 48283, 51643, 54763, 58507
21	85	A046018	431, 503, 743, 863, 1931, 2503, 2579, 2767, 2819, 3011, 3371, 4283, 4523, 4691, 5011, 5647, 5851, 5867, 6323, 6691, 7907, 8059, 8123, 8171, 8243, 8387, 8627, 8747, 9091, 9187, 9811, 9859, 10067, 10771, 11731, 12107, 12547, 13171, 13291, 13339, 13723, 14419, 14563, 15427, 16339, 16987, 17107, 17707, 17971, 18427, 18979, 19483, 19531, 19819, 20947, 21379, 22027, 22483, 22963, 23227, 23827, 25603, 26683, 27427, 28387, 28723, 28867, 31963, 32803, 34147, 34963, 35323, 36067, 36187, 39043, 40483, 44683, 46027, 49603, 51283, 52627, 55603, 58963, 59467, 61483
22	139	A171724	591, 623, 767, 871, 879, 1076, 1111, 1167, 1304, 1556, 1591, 1639, 1903, 2215, 2216, 2263, 2435, 2623, 2648, 2815, 2863, 2935, 3032, 3151, 3316, 3563, 3587, 3827, 4084, 4115, 4163, 4328, 4456, 4504, 4667, 4811, 5383, 5416, 5603, 5716, 5739, 5972, 6019, 6127, 6243, 6616, 6772, 6819, 7179, 7235, 7403, 7763, 7768, 7899, 8023, 8143, 8371, 8659, 8728, 8851, 8907, 8915, 9267, 9304, 9496, 10435, 10579, 10708, 10851, 11035, 11283, 11363, 11668, 12091, 12115, 12403, 12867, 13672, 14019, 14059, 14179, 14548, 14587, 14635, 15208, 15563, 15832, 16243, 16251, 16283, 16291, 16459, 17147, 17587, 17779, 17947, 18115, 18267, 18835, 18987, 19243, 19315, 19672, 20308, 20392, 22579, 22587, 22987, 24243, 24427, 25387, 25507, 25843, 25963, 26323, 26548, 27619, 28267, 29227, 29635, 29827, 30235, 30867, 31315, 33643, 33667, 34003, 34387, 35347, 41083, 43723, 44923, 46363, 47587, 47923, 49723, 53827, 77683, 85507
23	68	A046020	647, 1039, 1103, 1279, 1447, 1471, 1811, 1979, 2411, 2671, 3491, 3539, 3847, 3923, 4211, 4783, 5387, 5507, 5531, 6563, 6659, 6703, 7043, 9587, 9931, 10867, 10883, 12203, 12739, 13099, 13187, 15307, 15451, 16267, 17203, 17851, 18379, 20323, 20443, 20899, 21019, 21163, 22171, 22531, 24043, 25147, 25579, 25939, 26251, 26947, 27283, 28843, 30187, 31147, 31267, 32467, 34843, 35107, 37003, 40627, 40867, 41203, 42667, 43003, 45427, 45523, 47947, 90787
24	511	A048925	695, 759, 1191, 1316, 1351, 1407, 1615, 1704, 1736, 1743, 1988, 2168, 2184, 2219, 2372, 2408, 2479, 2660, 2696, 2820, 2824, 2852, 2856, 2915, 2964, 3059, 3064, 3127, 3128, 3444, 3540, 3560, 3604, 3620, 3720, 3864, 3876, 3891, 3899, 3912, 3940, 4063, 4292, 4308, 4503, 4564, 4580, 4595, 4632, 4692, 4715, 4744, 4808, 4872, 4920, 4936, 5016, 5124, 5172, 5219, 5235, 5236, 5252, 5284, 5320, 5348, 5379, 5432, 5448, 5555, 5588, 5620, 5691, 5699, 5747, 5748, 5768, 5828, 5928, 5963, 5979, 6004, 6008, 6024, 6072, 6083, 6132, 6180, 6216, 6251, 6295, 6340, 6411, 6531, 6555, 6699, 6888, 6904, 6916, 7048, 7108, 7188, 7320, 7332, 7348, 7419, 7512, 7531, 7563, 7620, 7764, 7779, 7928, 7960, 7972, 8088, 8115, 8148, 8211, 8260, 8328, 8344, 8392, 8499, 8603, 8628, 8740, 8760, 8763, 8772, 8979, 9028, 9048, 9083, 9112, 9220, 9259, 9268, 9347, 9352, 9379, 9384, 9395, 9451, 9480, 9492, 9652, 9672, 9715, 9723, 9823, 9915, 9928, 9940, 10011, 10059, 10068, 10120, 10180, 10187, 10212, 10248, 10283, 10355, 10360, 10372, 10392, 10452, 10488, 10516, 10612, 10632, 10699, 10740, 10756, 10788, 10792, 10840, 10852, 10923, 11019, 11032, 11139, 11176, 11208, 11211, 11235, 11267, 11307, 11603, 11620, 11627, 11656, 11667, 11748, 11752, 11811, 11812, 11908, 11928, 12072, 12083, 12243, 12292, 12376, 12408, 12435, 12507, 12552, 12628, 12760, 12808, 12820, 12891, 13035, 13060, 13080, 13252, 13348, 13395, 13427, 13444, 13512, 13531, 13539, 13540, 13587, 13611, 13668, 13699, 13732, 13780, 13912, 14035, 14043, 14212, 14235, 14260, 14392, 14523, 14532, 14536, 14539, 14555, 14595, 14611, 14632, 14835, 14907, 14952, 14968, 14980, 15019, 15112, 15267, 15339, 15411, 15460, 15483, 15528, 15555, 15595, 15640, 15652, 15747, 15748, 15828, 15843, 15931, 15940, 15988, 16107, 16132, 16315, 16360, 16468, 16563, 16795, 16827, 16872, 16888, 16907, 16948, 17032, 17043, 17059, 17092, 17283, 17560, 17572, 17620, 17668, 17752, 17812, 17843, 18040, 18052, 18088, 18132, 18148, 18340, 18507, 18568, 18579, 18595, 18627, 18628, 18667, 18763, 18795, 18811, 18867, 18868, 18915, 19203, 19528, 19579, 19587, 19627, 19768, 19803, 19912, 19915, 20260, 20307, 20355, 20427, 20491, 20659, 20692, 20728, 20803, 20932, 20955, 20980, 20995, 21112, 21172, 21352, 21443, 21448, 21603, 21747, 21963, 21988, 22072, 22107, 22180, 22323, 22339, 22803, 22852, 22867, 22939, 23032, 23035, 23107, 23115, 23188, 23235, 23307, 23368, 23752, 23907, 23995, 24115, 24123, 24292, 24315, 24388, 24595, 24627, 24628, 24643, 24915, 24952, 24955, 25048, 25195, 25347, 25467, 25683, 25707, 25732, 25755, 25795, 25915, 25923, 25972, 25987, 26035, 26187, 26395, 26427, 26467, 26643, 26728, 26995, 27115, 27163, 27267, 27435, 27448, 27523, 27643, 27652, 27907, 28243, 28315, 28347, 28372, 28459, 28747, 28891, 29128, 29283, 29323, 29395, 29563, 29659, 29668, 29755, 29923, 30088, 30163, 30363, 30387, 30523, 30667, 30739, 30907, 30955, 30979, 31252, 31348, 31579, 31683, 31795, 31915, 32008, 32043, 32155, 32547, 32635, 32883, 33067, 33187, 33883, 34203, 34363, 34827, 34923, 36003, 36043, 36547, 36723, 36763, 36883, 37227, 37555, 37563, 38227, 38443, 38467, 39603, 39643, 39787, 40147, 40195, 40747, 41035, 41563, 42067, 42163, 42267, 42387, 42427, 42835, 43483, 44947, 45115, 45787, 46195, 46243, 46267, 47203, 47443, 47707, 48547, 49107, 49267, 49387, 49987, 50395, 52123, 52915, 54307, 55867, 56947, 57523, 60523, 60883, 61147, 62155, 62203, 63043, 64267, 79363, 84043, 84547, 111763
25	95	A056987	479, 599, 1367, 2887, 3851, 4787, 5023, 5503, 5843, 7187, 7283, 7307, 7411, 8011, 8179, 9227, 9923, 10099, 11059, 11131, 11243, 11867, 12211, 12379, 12451, 12979, 14011, 14923, 15619, 17483, 18211, 19267, 19699, 19891, 20347, 21107, 21323, 21499, 21523, 21739, 21787, 21859, 24091, 24571, 25747, 26371, 27067, 27091, 28123, 28603, 28627, 28771, 29443, 30307, 30403, 30427, 30643, 32203, 32443, 32563, 32587, 33091, 34123, 34171, 34651, 34939, 36307, 37363, 37747, 37963, 38803, 39163, 44563, 45763, 48787, 49123, 50227, 51907, 54667, 55147, 57283, 57667, 57787, 59707, 61027, 62563, 63067, 64747, 66763, 68443, 69763, 80347, 85243, 89083, 93307

The number of negative discriminants having class number 1, 2, 3, ... are 9, 18, 16, 54, 25, 51, 31, ... (OEIS A046125). The largest negative discriminants having class numbers 1, 2, 3, ... are 163, 427, 907, 1555, 2683, ... (OEIS A038552).

The discriminants 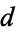 corresponding to real quadratic fields are 5, 8, 12, 13, 17, 21, 24, 28, 29, 33, 37, 40, 41, 44, 53, ... (OEIS A003658), corresponding to class numbers 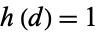, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, ... (OEIS A003652).

The table below gives lists of the first few positive fundamental discriminants 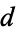 having small class numbers 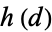, corresponding to real quadratic fields, augmenting the table of Cohn (1980, pp. 271-274) by including terms divisible by 4 (Cohen 1993, pp. 516-519; Cohen 2000, pp. 534-537). In fact, the discriminant of all quadratic number fields is squarefree except for a possible factor of 4.

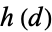	OEIS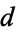
1	A003656	5, 8, 12, 13, 17, 21, 24, 28, 29, 33, 37, 41, 44, 53, 56, 57, 61, ...
2	A094619	40, 60, 65, 85, 104, 105, 120, 136, 140, 156, 165, 168, 185, 204, ...
3	A094612	229, 257, 316, 321, 469, 473, 568, 733, 761, 892, 993, 1016, 1101, ...
4	A094613	145, 328, 445, 505, 520, 680, 689, 777, 780, 793, 840, 876, 897, 901, ...
5	A094614	401, 817, 1093, 1393, 1429, 1641, 1756, 1897, 1996, 2081, 2153, 2908, ...

The smallest 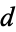 such that the real quadratic field with discriminant  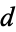has class  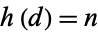for 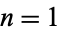, 2, ... are 5, 40, 229, 145, 401, 697, 577, 904, 1129, ... (OEIS A081364).

REFERENCES:

Arno, S. "The Imaginary Quadratic Fields of Class Number 4." Acta Arith. 40, 321-334, 1992.

Arno, S.; Robinson, M. L.; and Wheeler, F. S. "Imaginary Quadratic Fields with Small Odd Class Number." http://www.math.uiuc.edu/Algebraic-Number-Theory/0009/.

Buell, D. A. "Small Class Numbers and Extreme Values of 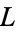-Functions of Quadratic Fields." Math. Comput. 139, 786-796, 1977.

Cohen, H. "Table of Class Numbers of Complex Quadratic Fields" and "Table of Class Numbers and Units of Real Quadratic Fields." §B.1 and B.2 in A Course in Computational Algebraic Number Theory. New York: Springer-Verlag, pp. 513-519, 1993.

Cohen, H. "Hilbert Class Fields of Quadratic Fields." §12.1 in Advanced Topics in Computational Number Theory. New York: Springer-Verlag, pp. 533-542, 2000.

Cohn, H. Advanced Number Theory. New York: Dover, pp. 163 and 234, 1980.

Cox, D. A. Primes of the Form x2+ny2: Fermat, Class Field Theory and Complex Multiplication. New York: Wiley, 1997.

Davenport, H. "Dirichlet's Class Number Formula." Ch. 6 in Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, pp. 43-53, 1980.

Finch, S. R. "Class Number Theory." http://algo.inria.fr/csolve/clss.pdf.

Himmetoglu, S. Berechnung von Klassenzahlen Imaginaer-Quadratischer Zahlkörper. Diplomarbeit. Heidelberg, Germany: University of Heidelberg Faculty for Mathematics, March 1986.

Iyanaga, S. and Kawada, Y. (Eds.). "Class Numbers of Algebraic Number Fields." Appendix B, Table 4 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1494-1496, 1980.

Montgomery, H. and Weinberger, P. "Notes on Small Class Numbers." Acta. Arith. 24, 529-542, 1974.

Müller, H. "A Calculation of Class-Numbers of Imaginary Quadratic Numberfields." Tamkang J. Math. 9, 121-128, 1978.

Oesterlé, J. "Nombres de classes des corps quadratiques imaginaires." Astérique 121-122, 309-323, 1985.

Sloane, N. J. A. Sequences A003652/M0051, A003656/M3777, A003657/M2332, A003658/M3776, A006203/M5131, A006641/M0112, A013658, A014602, A014603, A035120, A038552, A046002, A046003, A046125, A048925, A056987, A081364, A094612, A094613, A094614, and A094619 in "The On-Line Encyclopedia of Integer Sequences."

Stark, H. M. "A Complete Determination of the Complex Quadratic Fields of Class Number One." Michigan Math. J. 14, 1-27, 1967.

Stark, H. M. "On Complex Quadratic Fields with Class Number Two." Math. Comput. 29, 289-302, 1975.

Wagner, C. "Class Number 5, 6, and 7." Math. Comput. 65, 785-800, 1996.