Kolakoski Sequence

The self-describing sequence consisting of "blocks" of single and double 1s and 2s, where a "block" is a single digit or pair of digits that is different from the digit (or pair of digits) in the preceding block. To construct the sequence, start with the single digit 1 (the first "block"). Here, the single 1 means that block of length one follows the first block. Therefore, require that the next block is 2, giving the sequence 12.

Now, the 2 means that the next (third) block will have length two, so append 11 and obtain the sequence 1211. We have added two 1s, so the fourth and fifth blocks have length one each, giving 12112 and then 121121. As a result of adding 21, we obtain 121121221. As a result of adding 221, we obtain 12112122122112, and so on, giving the sequence 1, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, ... (OEIS A006928). The sequence after successive iterations is given by 1, 12, 1211, 121121, 121121221, ..., and the lengths of this sequence after steps , 2, ... are given by 1, 2, 4, 6, 9, 14, 22, ... (OEIS A042942).

If the sequence is started with 1, 2, 2 and the above procedure is undertaken beginning with the last 2, then the virtually identical sequence 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, ... (OEIS A000002) is obtained. (It is the same as OEIS A006928, except that the second 2 is doubled.) When presented in this form, the term 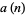 gives the length of the 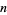th run in the sequence. The lengths after steps 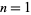, 2, ... are then 1, 2, 3, 5, 7, 10, 15, ... (OEIS A001083), essentially one less than OEIS A042942.

A recurrence plot of the Kolakoski sequence is illustrated above.

The constant obtained by taking 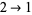, , 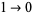and interpreting the result as a binary fraction

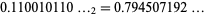(OEIS A118270) is sometimes known as the Kolakoski constant (Plouffe).

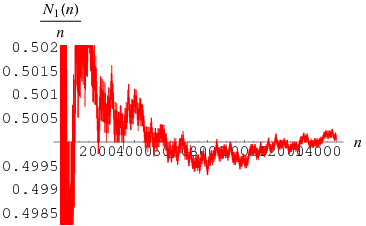
The question of whether the number of 1s is "asymptotically" equal to the number of 2s is unsettled, although the above plot (which shows the fraction of 1s as a function of number of digits) is certainly consistent with 1 and 2 being equidistributed.

REFERENCES:
Allouche, J.-P. and Shallit, J. Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 336-337, 2003.

Dekking, F. M. "On the Structure of Self-Generating Sequences." In Séminaire de Théorie des Nombres, 1980-1981. Held at the Université de Bordeaux I, Talence, during the academic year 1980-1981. Université de Bordeaux I, U.E.R. de Mathématiques et d'Informatique, Laboratoire de Théorie des Nombres, Talence, pp. 1-6, 1981.

Dekking, F. M. "What Is the Long Range Order in the Kolakoski Sequence?" In Proceedings of the NATO Advanced Study Institute held in Waterloo, ON, August 21-September 1, 1995 (Ed. R. V. Moody). Dordrecht, Netherlands: Kluwer, pp. 115-125, 1997.

Keane, M. S. "Ergodic Theory and Subshifts of Finite Type." In Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces (Ed. T. Bedford and M. Keane). Oxford, England: Oxford University Press, pp. 35-70, 1991.

Kimberling, C. "Integer Sequences and Arrays." http://faculty.evansville.edu/ck6/integer/.

Kimberling, C. "Unsolved Problems and Rewards." http://faculty.evansville.edu/ck6/integer/unsolved.html.

Kolakoski, W. "Problem 5304: Self Generating Runs." Amer. Math. Monthly 72, 674, 1965.

Kolakoski, W. "Problem 5304." Amer. Math. Monthly 73, 681-682, 1966.

Lagarias, J. C. "Number Theory and Dynamical Systems." In The Unreasonable Effectiveness of Number Theory (Ed. S. A. Burr). Providence, RI: Amer. Math. Soc., pp. 35-72, 1992.

Paun, G. and Salomaa, A. "Self-Reading Sequences." Amer. Math. Monthly 103, 166-168, 1996.

Plouffe, S. "Kolakoski Constant to 25000 Digits." http://pi.lacim.uqam.ca/piDATA/Kolakoski.txt.

Sellke. Problem 324 in Statistica Neerlandica 50, 222-223, 1996.

Sloane, N. J. A. Sequences A000002/M0190, A001083, A006298/M0070, A042942, and A118270 in "The On-Line Encyclopedia of Integer Sequences."

Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, p. 233, 1991.