


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 8-1-2020
Date: 30-1-2021
Date: 20-10-2019
|
Following Ramanujan (1913-1914), write
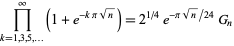 |
(1) |
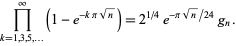 |
(2) |
These satisfy the equalities
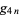 |
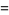 |
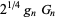 |
(3) |
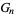 |
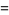 |
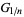 |
(4) |
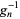 |
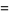 |
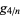 |
(5) |
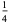 |
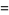 |
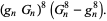 |
(6) |
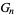 and
and 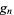 can be derived using the theory of modular functions and can always be expressed as roots of algebraic equations when
can be derived using the theory of modular functions and can always be expressed as roots of algebraic equations when 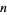 is rational. They are related to the Weber functions.
is rational. They are related to the Weber functions.
For simplicity, Ramanujan tabulated 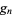 for
for 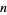 even and
even and 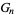 for
for 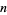 odd. However, (6) allows
odd. However, (6) allows 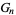 and
and 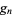 to be solved for in terms of
to be solved for in terms of 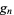 and
and 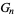 , giving
, giving
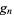 |
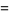 |
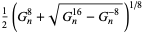 |
(7) |
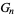 |
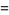 |
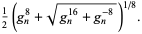 |
(8) |
Using (◇) and the above two equations allows 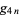 to be computed in terms of
to be computed in terms of 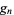 or
or 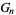
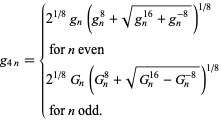 |
(9) |
In terms of the parameter 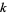 and complementary parameter
and complementary parameter 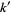 ,
,
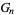 |
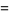 |
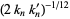 |
(10) |
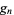 |
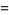 |
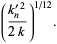 |
(11) |
Here,
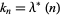 |
(12) |
is the elliptic lambda function, which gives the value of 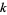 for which
for which
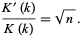 |
(13) |
Solving for 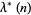 gives
gives
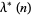 |
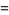 |
![1/2[sqrt(1+G_n^(-12))-sqrt(1-G_n^(-12))]](http://mathworld.wolfram.com/images/equations/Ramanujang-andG-Functions/Inline45.gif) |
(14) |
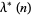 |
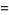 |
![g_n^6[sqrt(g_n^(12)+g_n^(-12))-g_n^6].](http://mathworld.wolfram.com/images/equations/Ramanujang-andG-Functions/Inline48.gif) |
(15) |
Solving for 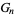 and
and 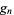 directly in terms of
directly in terms of 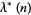 then gives
then gives
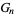 |
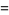 |
![2^(-1/12)[lambda^*^2(n)-lambda^*^4(n)]^(-1/24)](http://mathworld.wolfram.com/images/equations/Ramanujang-andG-Functions/Inline54.gif) |
(16) |
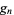 |
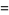 |
![2^(-1/12)[1/(lambda^*(n))-lambda^*(n)]^(1/12).](http://mathworld.wolfram.com/images/equations/Ramanujang-andG-Functions/Inline57.gif) |
(17) |
Analytic values for small values of 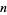 can be found in Ramanujan (1913-1914) and Borwein and Borwein (1987), and have been compiled by Weisstein. Ramanujan (1913-1914) contains a typographical error labeling
can be found in Ramanujan (1913-1914) and Borwein and Borwein (1987), and have been compiled by Weisstein. Ramanujan (1913-1914) contains a typographical error labeling 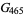 as
as 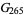 .
.
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 139 and 298, 1987.
Ramanujan, S. "Modular Equations and Approximations to 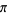 ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|