


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-11-2019
Date: 20-11-2019
Date: 20-2-2020
|
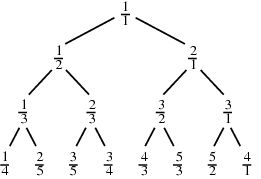
A special type of binary tree obtained by starting with the fractions 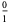 and
and 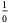 and iteratively inserting
and iteratively inserting 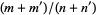 between each two adjacent fractions
between each two adjacent fractions 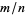 and
and 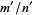 . The result can be arranged in tree form as illustrated above. The Farey sequence
. The result can be arranged in tree form as illustrated above. The Farey sequence 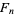 defines a subtree of the Stern-Brocot tree obtained by pruning off unwanted branches (Vardi 1991, Graham et al. 1994).
defines a subtree of the Stern-Brocot tree obtained by pruning off unwanted branches (Vardi 1991, Graham et al. 1994).
REFERENCES:
Bogomolny, A. "Stern-Brocot Tree." http://www.cut-the-knot.org/blue/Stern.shtml.
Brocot, A. "Calcul des rouages par approximation, nouvelle méthode." Revue Chonométrique 3, 186-194, 1861.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 116-117, 1994.
Haynes, B. "On the Teeth of Wheels." American Scientist 88, No. 4, July-August 2000. http://www.americanscientist.org/template/AssetDetail/assetid/20826.
Stern, M. A. "Über eine zahlentheoretische Funktion." J. reine angew. Math. 55, 193-220, 1858.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, p. 253, 1991.
Viswanath, D. "Random Fibonacci Sequences and the Number 1.13198824...." Math. Comput. 69, 1131-1155, 2000.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|