


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-8-2018
Date: 1-10-2019
Date: 25-3-2019
|
Polynomials 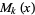 which form the associated Sheffer sequence for
which form the associated Sheffer sequence for
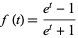 |
(1) |
and have the generating function
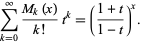 |
(2) |
An explicit formula is given by
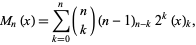 |
(3) |
where 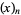 is a falling factorial, which can be summed in closed form in terms of the hypergeometric function, gamma function, and polygamma function. The binomial identity associated with the Sheffer sequence is
is a falling factorial, which can be summed in closed form in terms of the hypergeometric function, gamma function, and polygamma function. The binomial identity associated with the Sheffer sequence is
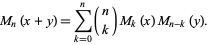 |
(4) |
The Mittag-Leffler polynomials satisfy the recurrence formula
![M_(n+1)(x)=1/2x[M_n(x+1)+2M_n(x)+M_n(x-1)].](http://mathworld.wolfram.com/images/equations/Mittag-LefflerPolynomial/NumberedEquation5.gif) |
(5) |
The first few Mittag-Leffler polynomials are
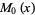 |
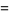 |
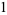 |
(6) |
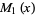 |
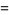 |
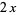 |
(7) |
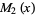 |
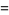 |
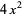 |
(8) |
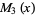 |
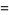 |
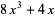 |
(9) |
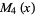 |
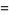 |
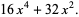 |
(10) |
The Mittag-Leffler polynomials 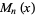 are related to the Pidduck polynomials by
are related to the Pidduck polynomials by
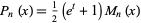 |
(11) |
(Roman 1984, p. 127).
REFERENCES:
Bateman, H. "The Polynomial of Mittag-Leffler." Proc. Nat. Acad. Sci. USA 26, 491-496, 1940.
Roman, S. "The Mittag-Leffler Polynomials." §4.1.6 in The Umbral Calculus. New York: Academic Press, pp. 75-78 and 127, 1984.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|