Gould Polynomial

The polynomials 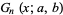 given by the associated Sheffer sequence with

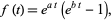(1)

where 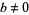. The inverse function (and therefore generating function) cannot be computed algebraically, but the generating function

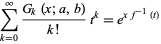(2)

can be given in terms of the sum

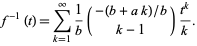(3)

This results in

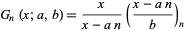(4)

where 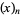 is a falling factorial. The first few are

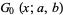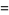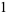			(5)
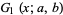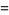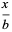			(6)
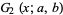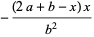			(7)
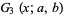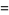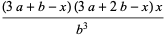			(8)
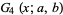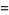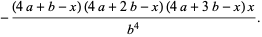			(9)

The binomial identity obtained from the Sheffer sequence gives the generalized Chu-Vandermonde identity

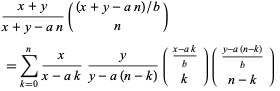(10)

(Roman 1984, p. 69; typo corrected).

In the special case 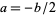, the function  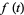simplifies to

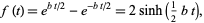(11)

which gives the generating function

(12)

giving the polynomials

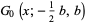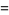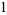			(13)
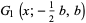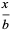			(14)
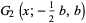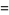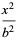			(15)
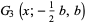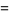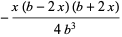			(16)
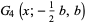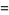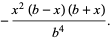			(17)

REFERENCES:

Gould, H. W. "Note on a Paper of Sparre-Anderson." Math. Scand. 6, 226-230, 1958.

Gould, H. W. "Stirling Number Representation Problems." Proc. Amer. Math. Soc. 11, 447-451, 1960.

Gould, H. W. "A Series of Transformation for Finding Convolution Identities." Duke Math. J. 28, 193-202, 1961.

Gould, H. W. "Note on a Paper of Klamkin Concerning Stirling Numbers." Amer. Math. Monthly 68, 477-479, 1961.

Gould, H. W. "A New Convolution Formula and Some New Orthogonal Relations for the Inversion of Series." Duke Math. J. 29, 393-404, 1962.

Gould, H. W. "Congruences Involving Sums of Binomial Coefficients and a Formula of Jensen." Amer. Math. Monthly 69, 400-402, 1962.

Roman, S. "The Gould Polynomials and he Central Factorial Polynomials." §4.1.4 in The Umbral Calculus. New York: Academic Press, pp. 67-70, 1984.

Rota, G.-C.; Kahaner, D.; Odlyzko, A. "On the Foundations of Combinatorial Theory. VIII: Finite Operator Calculus." J. Math. Anal. Appl. 42, 684-760, 1973.