


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-7-2019
Date: 17-3-2019
Date: 19-5-2019
|
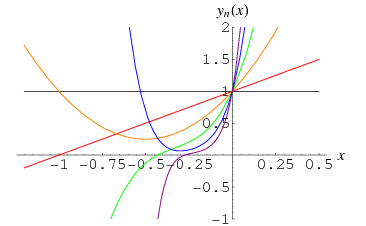
Krall and Fink (1949) defined the Bessel polynomials as the function
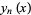 |
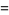 |
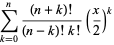 |
(1) |
 |
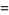 |
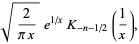 |
(2) |
where 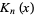 is a modified Bessel function of the second kind. They are very similar to the modified spherical bessel function of the second kind
is a modified Bessel function of the second kind. They are very similar to the modified spherical bessel function of the second kind 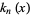 . The first few are
. The first few are
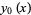 |
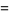 |
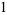 |
(3) |
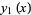 |
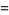 |
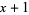 |
(4) |
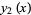 |
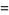 |
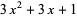 |
(5) |
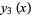 |
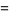 |
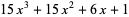 |
(6) |
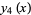 |
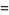 |
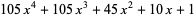 |
(7) |
(OEIS A001497). These functions satisfy the differential equation
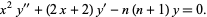 |
(8) |
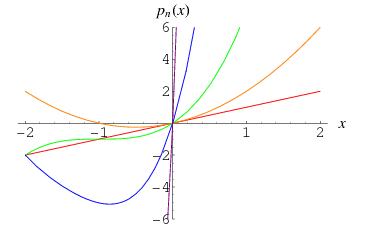
Carlitz (1957) subsequently considered the related polynomials
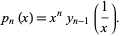 |
(9) |
This polynomial forms an associated Sheffer sequence with
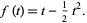 |
(10) |
This gives the generating function
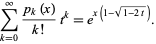 |
(11) |
The explicit formula is
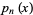 |
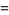 |
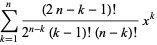 |
(12) |
 |
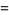 |
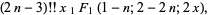 |
(13) |
where 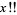 is a double factorial and
is a double factorial and 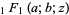 is a confluent hypergeometric function of the first kind. The first few polynomials are
is a confluent hypergeometric function of the first kind. The first few polynomials are
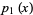 |
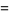 |
 |
(14) |
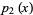 |
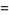 |
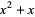 |
(15) |
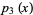 |
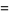 |
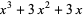 |
(16) |
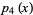 |
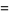 |
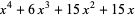 |
(17) |
(OEIS A104548).
The polynomials satisfy the recurrence formula
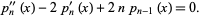 |
(18) |
REFERENCES:
Carlitz, L. "A Note on the Bessel Polynomials." Duke Math. J. 24, 151-162, 1957.
Grosswald, E. Bessel Polynomials. New York: Springer-Verlag, 1978.
Krall, H. L. and Fink, O. "A New Class of Orthogonal Polynomials: The Bessel Polynomials." Trans. Amer. Math. Soc. 65, 100-115, 1949.
Roman, S. "The Bessel Polynomials." §4.1.7 in The Umbral Calculus. New York: Academic Press, pp. 78-82, 1984.
Sloane, N. J. A. Sequences A001497, A001498, and A104548 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|