


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-10-2018
Date:
Date: 21-9-2018
|
The Riemann-Siegel integral formula is the following representation of the xi-function 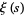 found in Riemann's Nachlass by Bessel-Hagen in 1926 (Siegel 1932; Edwards 2001, p. 166). The formula is essentially
found in Riemann's Nachlass by Bessel-Hagen in 1926 (Siegel 1932; Edwards 2001, p. 166). The formula is essentially
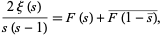 |
(1) |
where
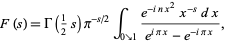 |
(2) |
the symbol 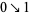 means that the path of integration is a line of slope
means that the path of integration is a line of slope 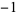 crossing the real axis between 0 and 1 and directed from upper left to lower right and in which
crossing the real axis between 0 and 1 and directed from upper left to lower right and in which 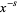 is defined on the slit plane (excluding 0 and negative real numbers) by taking
is defined on the slit plane (excluding 0 and negative real numbers) by taking 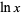 to be real on the positive real axis and setting
to be real on the positive real axis and setting 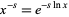 (Edwards 2001, p. 167). Here,
(Edwards 2001, p. 167). Here, 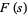 is analytic ar
is analytic ar 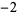 ,
, 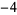 , ..., and has a simple pole at 0.
, ..., and has a simple pole at 0.
This formula gives a proof of the functional equation
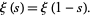 |
(3) |
REFERENCES:
Edwards, H. M. "Riemann-Siegel Integral Formula" and "Alternative Proof of the Integral Formula." §7.9 and 12.6 in Riemann's Zeta Function. New York: Dover, pp. 165-170 and 273-278, 2001.
Kuzmin, R. "On the Roots of Dirichlet Series." Izv. Akad. Nauk SSSR Ser. Math. Nat. Sci. 7, 1471-1491, 1934.
Siegel, C. L. "Über Riemanns Nachlaß zur analytischen Zahlentheorie." Quellen Studien zur Geschichte der Math. Astron. und Phys. Abt. B: Studien 2, 45-80, 1932. Reprinted in Gesammelte Abhandlungen, Vol. 1. Berlin: Springer-Verlag, 1966.ش



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|