Zagier's Identity

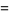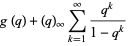			(1)
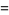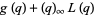			(2)
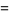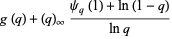			(3)
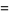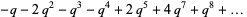			(4)

(OEIS A117586; Andrews 1972, 1998; Knuth and Paterson 1978; Chapman 2000; Zagier 2001), where

(5)

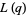 is a Lambert series, and  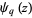is a q-polygamma function.

If

(6)

then a related identity is given by

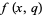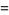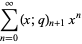			(7)
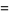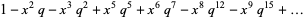			(8)

(Subbarao 1971, Andrews 1972, Andrews 1983, Knuth and Paterson 1978, Chapman 2000, Zagier 2001).

REFERENCES:

Andrews, G. E. "Two Theorems of Gauss and Allied Identities Proved Arithmetically." Pacific J. Math. 41, 563-578, 1972.

Andrews, G. E. "Euler's Pentagonal Number Theorem." Math. Mag. 56, 279-284, 1983.

Andrews, G. E. The Theory of Partitions. Cambridge, England: Cambridge University Press, 1998.

Chapman, R. "Franklin's Argument Proves an Identity of Zagier." Electronic J. Combinatorics 7, No. 1, R54, 1-5, 2000. http://www.combinatorics.org/Volume_7/Abstracts/v7i1r54.html.

Knuth, D. E. and Paterson, M. S. "Identities from Partition Involutions." Fib. Quart. 16, 198-212, 1978.

Sloane, N. J. A. Sequence A117586 in "The On-Line Encyclopedia of Integer Sequences."

Subbarao, M. V. "Combinatorial Proofs of Some Identities." Proc. Washington State University Conference on Number Theory. Washington State University, pp. 80-91, 1971.

Zagier, D. "Vassiliev Invariants and a Strange Identity Related to the Dedekind Eta-Function." Topology 40, 945-960, 2001.