المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Andrews-Schur Identity |
 1794
 05:57 مساءً
date: 21-8-2019 |
Author : Andrews, G. E. 
Book or Source : "A Polynomial Identity which Implies the Rogers-Ramanujan Identities." Scripta Math. 28 
Page and Part : ...|
Read More
Date: 23-8-2019
2586
Date: 14-10-2019
1520
Date: 25-4-2019
1921
|
The Andrews-Schur identity states
![sum_(k=0)^nq^(k^2+ak)[2n-k+a; k]_q
=sum_(k=-infty)^inftyq^(10k^2+(4a-1)k)[2n+2a+2; n-5k]_q([10k+2a+2]_q)/([2n+2a+2]_q)](http://mathworld.wolfram.com/images/equations/Andrews-SchurIdentity/NumberedEquation1.gif) |
(1) |
where ![[n; m]_q](http://mathworld.wolfram.com/images/equations/Andrews-SchurIdentity/Inline1.gif)
is a q-binomial coefficient and ![[n]_q](http://mathworld.wolfram.com/images/equations/Andrews-SchurIdentity/Inline2.gif)
is a q-bracket. It is a polynomial identity for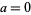 
, 1 which implies the Rogers-Ramanujan identities by taking 
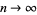and applying the Jacobi triple product identity.
The limit as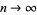 
of the identity in (1) is
 |
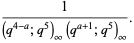(2) |
A variant of the identity is
![sum_(k=-|_a/2_|)^nq^(k^2+2ak)[n+k+a; n-k]_q
=sum_(-|_(n+2a+2)/5_|)^(|_n/5_|)q^(15k^2+(6a+1)k)[2n+2a+2; n-5k]_q([10k+2a+2]_q)/([2n+2a+2]_q),](http://mathworld.wolfram.com/images/equations/Andrews-SchurIdentity/NumberedEquation3.gif) |
(3) |
where the symbol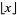 
in the sum limits is the floor function (Paule 1994). A related identity is given by
 |
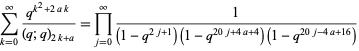(4) |
for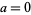 
, 1 (Paule 1994). For 
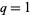, equation (3) becomes
 |
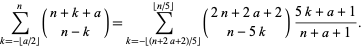(5) |
REFERENCES:
Andrews, G. E. "A Polynomial Identity which Implies the Rogers-Ramanujan Identities." Scripta Math. 28, 297-305, 1970.
Paule, P. "Short and Easy Computer Proofs of the Rogers-Ramanujan Identities and of Identities of Similar Type." Electronic J. Combinatorics 1, No. 1, R10, 1-9, 1994. http://www.combinatorics.org/Volume_1/Abstracts/v1i1r10.html.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة توجه دعوة لجامعة القادسية للمشاركة في حفل التخرج المركزي
|
|
|
