


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-10-2019
Date: 24-6-2019
Date: 4-1-2016
|
Jonquière's relation, sometimes also spelled "Joncquière's relation" (Erdélyi et al. 1981, p. 31), states
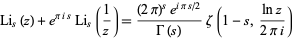 |
Erdélyi et al. (1981, p. 31), where 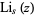 is a polylogarithm,
is a polylogarithm, 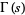 is the gamma function, and
is the gamma function, and 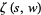 is the Hurwitz zeta function, and
is the Hurwitz zeta function, and 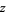 is not a member of the real interval
is not a member of the real interval ![[0,1]](http://mathworld.wolfram.com/images/equations/JonquieresRelation/Inline5.gif) .
.
The most general form of the identity valid everywhere in the complex plane is
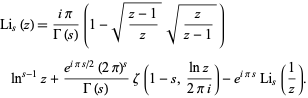 |
REFERENCES:
Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. Higher Transcendental Functions, Vol. 1. New York: Krieger, p. 31, 1981.
Jonquière, A. "Note sur la série 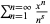 ." Bull. Soc. Math. France 17, 142-152, 1889.
." Bull. Soc. Math. France 17, 142-152, 1889.
Sondow, J. and Hadjicostas, P. "The Generalized-Euler-Constant Function 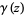 and a Generalization of Somos's Quadratic Recurrence Constant." 16 Oct 2006. http://arxiv.org/abs/math.CA/0610499.
and a Generalization of Somos's Quadratic Recurrence Constant." 16 Oct 2006. http://arxiv.org/abs/math.CA/0610499.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|